Integrated Modelling, Analysis and Optimization for Cyber-Physical Power Systems Considering the Impacts of Communication Networks
AUTHORS
L. XU - Department of Electrical Engineering, Tsinghua University, Beijing, China - Department of Civil and Environmental Engineering, Princeton University, NJ, USA
Q. GUO - Department of Electrical Engineering, Tsinghua University, Beijing, China

Summary
This paper summarizes the Ph. D. research work carried out by Luo Xu on modern power systems with the in-depth interdependence of physical power grids and cyber communication systems, that is, cyber-physical power systems (CPPSs). Such interdependence brings great challenges to the security, resilience and stability of CPPSs. This research work first establishes a hybrid information-energy flow model for interdependent modelling and computation. Then, a resilient communication optimization for CPPS considering cyber-physical uncertainties is proposed based on two-stage robust optimization to alleviate the load loss of power grids in extreme scenarios. Third, the stability of the time-delayed CPS is analysed based on the proposed model with a critical eigenvalue tracking algorithm, and an accurate stable region of time-delayed CPPSs can be obtained efficiently. Finally, the proper discrete control period for clock-synchronized CPPS under asynchronous phenomenon is investigated based on the discrete information-energy flow model.
This research work has been further developed into two online cyber-physical risk assessment and management platforms and implemented in several real-world bulk power systems, supporting the risk analysis and resilient operation of these power systems equipped with advanced information systems.
Keywords
Cyber-physical systems - integrated modelling - optimization - stability - synchronization1. Introduction
Recent years have witnessed rapid development in the fields of communication, computation, and controlling and sensing technologies. The concept of the cyber-physical system (CPS) has also undergone rapid progress over the last few years and is considered as an emerging field that will be relevant to the next generation of engineered systems and that will drive the in-depth informatization, digitization, and intellectualization reform of the modern power system. To establish a low-carbon power system with renewable energy as the mainstay, digital transformation will be a critical measure to flexibly control and manage large-scale renewable energy generation. Accordingly, the revolutionary advances in electricity networks have caused the concept of the cyber-physical power system (CPPS) to become a focus for both industry and academia [1].
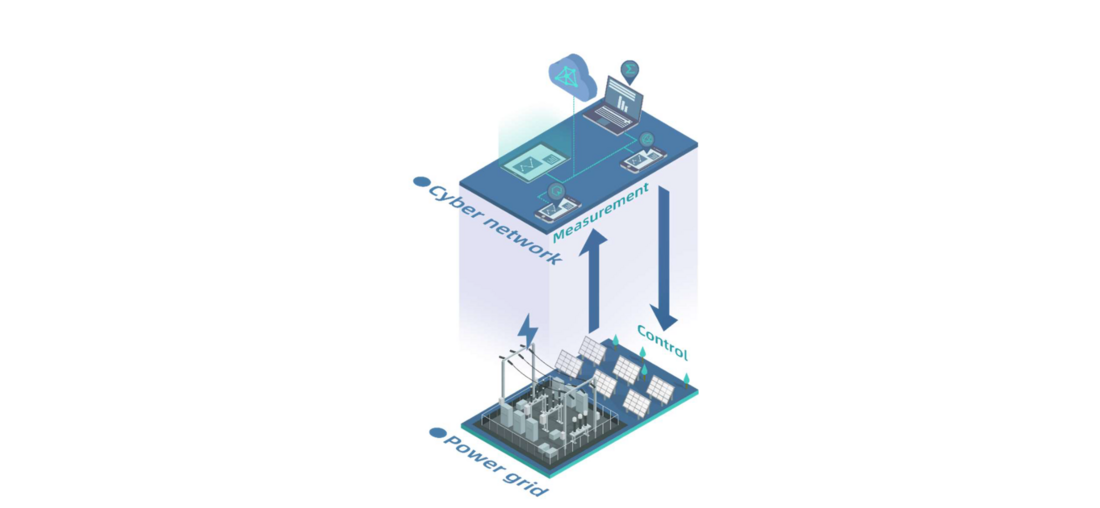
Figure 1 - Cyber-physical power systems
The interdependence of the cyber and physical spaces of a CPPS promotes the application of advanced information systems in system perception and operation and inversely induces the vulnerability superposition of the two spaces. Likewise, the broader boundary and more complicated environments of a CPPS bring great challenges to its operation and security. Over the past few decades, massive electricity outages induced by cyber accidents and disturbances have indicated the destructive power of the cyber system malfunction on power systems [2]. Moreover, when cyber information system and physical power system malfunctions occur simultaneously due to extreme hazards such as the 2106 Typhoon Meranti in Xiamen, China, as shown in Fig. 2, it may trigger a catastrophic cascading failure to the power system. These potential cyber-physical coupling failures alter the importance of studying the resilience of modern power systems from a cyber-physical perspective.
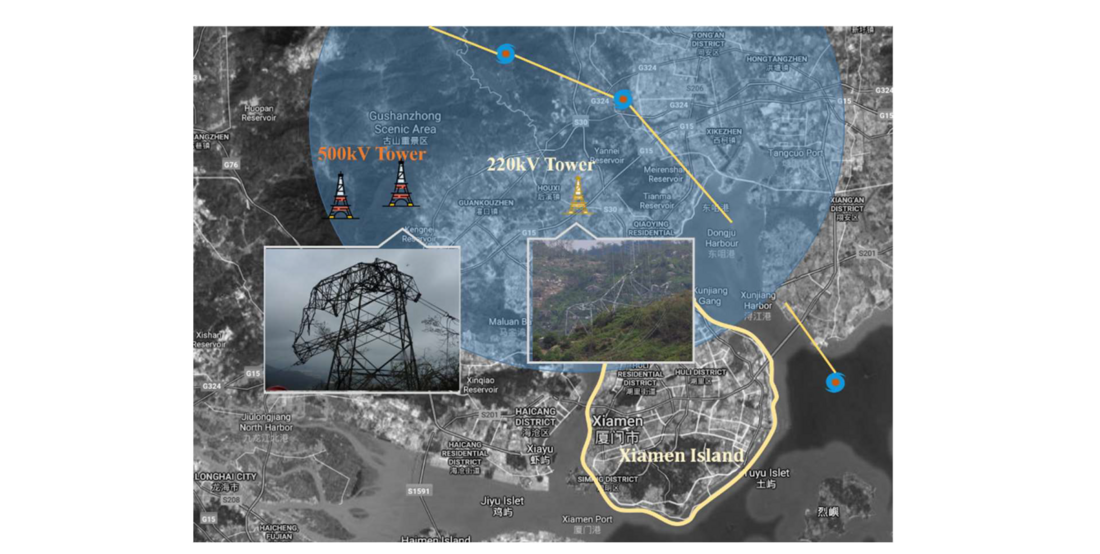
Figure 2 - Collapses of high-voltage transmission towers in Xiamen due to 2016 Typhoon Meranti
Against the in-depth interdependence of CPPS, it is critical to investigate the coupling mechanism, the interdependent analysis and optimization for modern power systems so as to ensure the safety and reliability of the operation of modern power systems embedded with advanced information systems. However, the traditional power system analysis and optimization focus on the physical system itself, and the impacts of the communication network are less considered. Due to the complicated heterogeneous characteristics of continuous dynamic power systems and discrete event-driven communication networks, the conventional model cannot be applied to the analysis of CPPS.
To address the above challenges, this Ph.D. thesis focuses on the integrated modelling, analysis and optimization of CPPSs considering the impacts of communication networks. Specifically, the Ph.D. research work makes the following contributions [1]-[9]:
- In Section 2, a framework and integrated hybrid system model of CPPS, named information-energy flow model, considering three-layer interdependences are proposed, which has been further developed into a cyber-physical security analysis platform for AGC in real-world bulk power systems. The model also lays the foundation for optimization and stability analysis.
- In Section 3, a communication routing optimization method for the resilience of CPPSs under cyber-physical disturbances is proposed with a priority mechanism that allocates reliable links to critical information flow. This optimized routing strategy has also been implemented in Guangdong Power Grid in China and can reduce the loss of load by up to nearly 60% in the worst scenario.
- In Section 4, the stability of CPPS with multiple time delays is analysed based on the dynamic information-energy flow model. A critical eigenvalue tracking algorithm is also proposed to determine the stability region of a time-delayed CPPS. The accuracy and efficiency of the model and the obtained stability region are verified by the simulation in a real-world distribution network.
- In Section 5, for clock-synchronization-based CPPSs with multiple controllers, a discrete cyber-physical state-transition equation considering the inevitable asynchronous phenomenon is proposed to analyse the stability of synchronized CPPSs. Then, the synchronous stability criterion is provided to determine the feasible synchronous control period of CPPSs.
2. Theory: Interdependent modelling and computation of CPPSs
2.1. Framework of interdependent CPPSs
The framework of interdependent CPPSs is proposed in our previous work [1]. The CPPS can be regarded as an in-depth coupled system of the cyber and physical spaces. Its cyber space is composed of communication networks and advanced information systems, including ubiquitous measurement, information transmission and processing, and decision-making activities. The physical space consists of the basic components of a power system and its energy flow. The cross-space interaction of information flow and energy flow makes the cyber and physical spaces tightly coupled.
The CPPS is defined as a set of elements, interconnections, and functions. Specifically, the objects in the set are described as follows:
- Elements: The elements in a CPPS refer to its components and facilities on both the cyber side and the physical side, such as power plants, substations, sensors, actuators, and optical cables. For modern power systems, some new participants, e.g., DERs, EVs, and humans, can also be regarded as elements in a CPPS.
- Interconnections: The interconnections construct power facilities and communication equipment into the power grid and the communication network, respectively, and achieve interaction between elements through energy flow and information flow. The integration of multi-agent renewable energy and EVs introduces the interconnections of social networks and transportation networks in a CPPS.
- Functions: The functions of a CPPS are related to many advanced information systems, such as the energy management system (EMS), to meet the electricity demand and the security of the power system. The functions are the driving forces to achieving deep integration between the cyber and physical spaces. In a modern power system with various participants, the functions of the electricity market and demand response further deepen the effects on the elements of CPPSs.
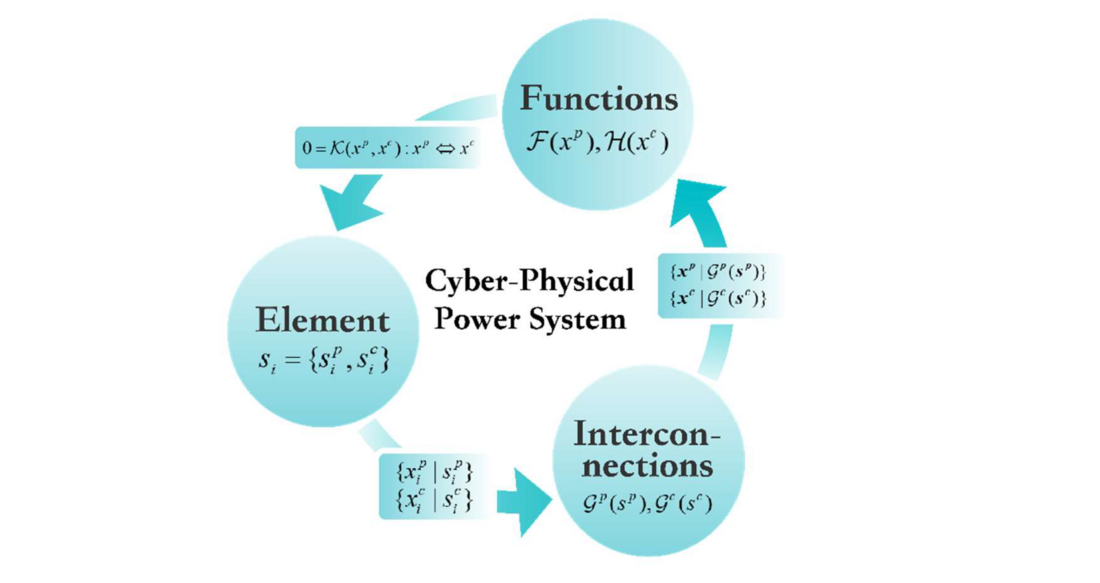
Figure 3 - The framework of a cyber-physical power system (CPPS) from a system-theory perspective
To clarify how elements, interconnections and functions constitute an operational CPPS with integrality, as shown in Fig. 3, where the subscript p and c denote the physical space and the cyber space. The relationships between these components of a CPPS are further explained as follows: (1) From elements s with state variables to interconnections
: Isolated, unconnected elements cannot form a system with integrality. The interconnections between the elements of a CPPS constitute the basic cyber-physical network structure, laying the foundation of carrying information and energy flow. (2) From interconnections to functions
on the physical side and
on the cyber side: The cyber-physical network with interconnections of elements needs to perform specific functions to form an operational system. For a CPPS, the functions can be regarded as the energy flow and information flow over physical power grids and information systems. (3) From functions to elements
: The functions, like the brain of a CPPS, perceive and control the state of the elements through the interconnections of information flow and energy flow, which is a critical relationship for a CPPS to maintain stability and the functional operation of the elements.
The key to the interdependence between the cyber space and the physical space lies in the interaction across space, which corresponds to the measurement and control links in the power cyber-physical system, and is reflected in the mapping relationship between information space and physical space:
(1)
2.2. Modelling and computation of interdependent CPPSs
The CPPS is a hybrid system with continuous time related to physical power systems and discrete time
related to the information control systems, where T is sampling period or synchronous control period and satisfies
.
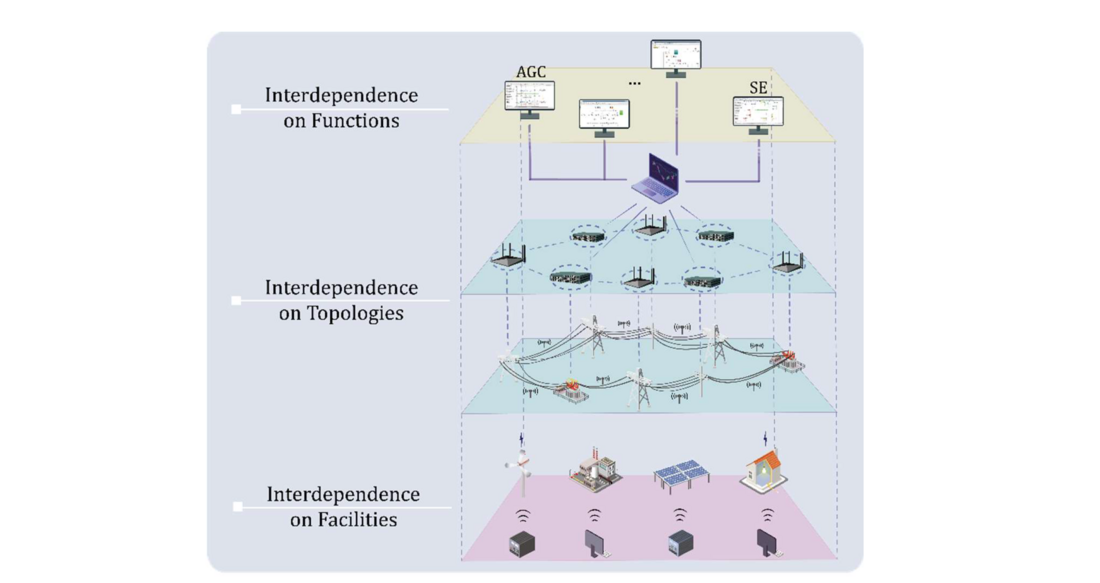
Figure 4 - Three-layer interdependences of a CPPS [1]
The physical power systems combined with a closed-loop information flow model is presented in our previous work [1], [3], [5]. Starting from the facility layer, a dynamical physical device equipped with its control system is considered as a cyber-physical system in the facility layer, which is described as the combination of the following differential algebraic equations.
(2)
where the measurement, decision and control execution activities are three major parts on the cyber side are modelled as the algebraic mapping from physical measurement variables to physical control variables in the form of discrete event-driven models.
In the topology layer, the information flow and power flow in the communication network and the power grid are established. In particular, the information flow model consists of information measurement, data transmission, data computing, decision making and execution. The path-branch incidence matrix method is used to describe the information flow model in [7]. Here we give an example of the proposed information flow model of the power flow correction control (PFCC) system as shown in Fig 5.
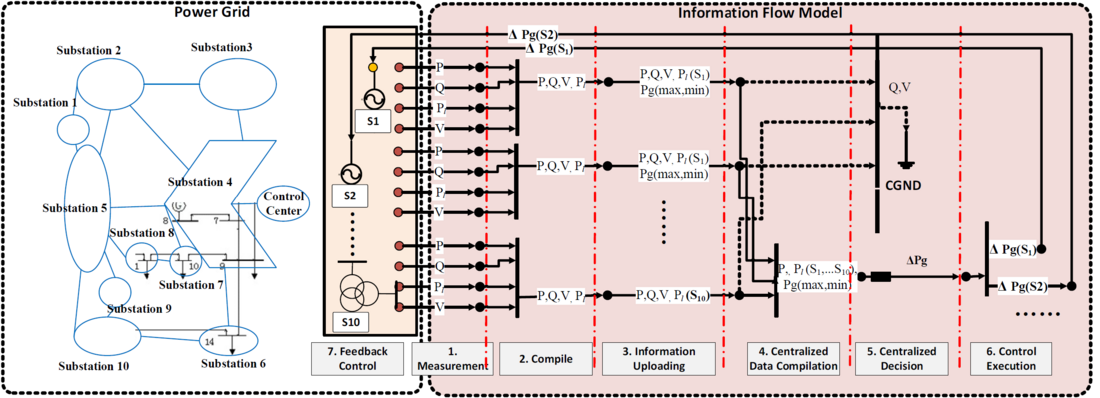
Figure 5 - Information flow model of PFCC system in a cyber-physical power system [7]
In the function layer, the decision-making activity on the cyber side makes the specific functions of information systems for power system operation realized. Thus, we proposed a closed-loop information-energy flow model in [1], [3] to describe the hybrid dynamical cyber-physical systems, as shown in Fig. 6. This model can be further expanded to consider the impacts of cyber disturbances on physical power systems and perform cyber-physical security analysis, stability analysis, and optimization.
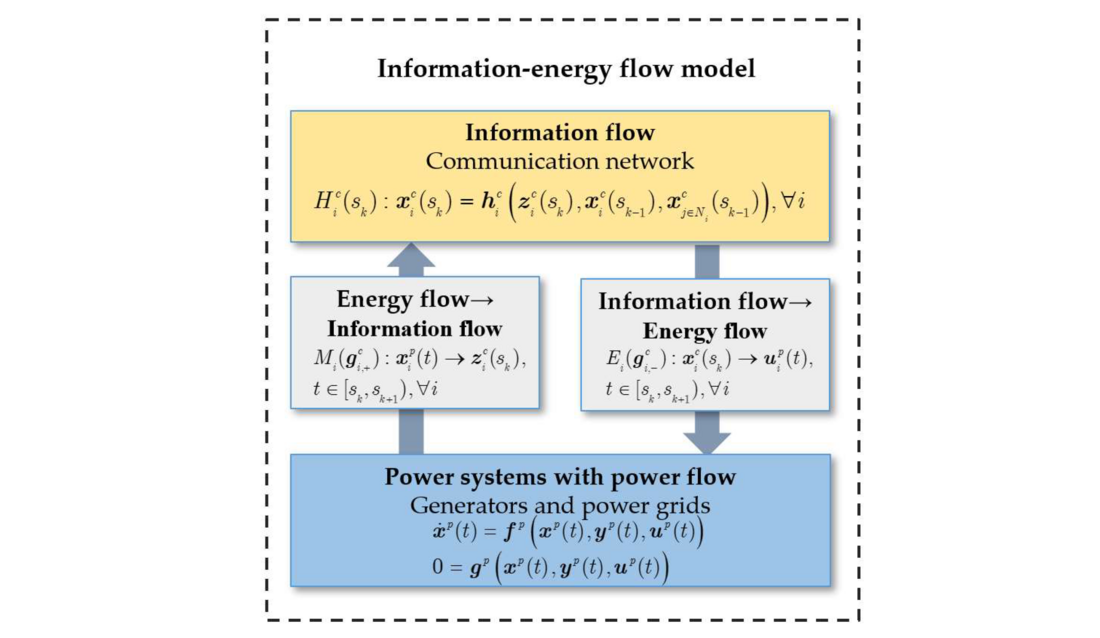
Figure 6 - Information-energy flow model for hybrid cyber-physical power systems [2]
2.3. Cyber-physical modelling and analysis in real-world power grids
The proposed information-energy flow model has been developed into the Cyber-Physical Monitoring and Control Systems (CPMCS) in Southwest of State Grid Corporation of China, which covers the three Chinese Provinces with nearly 20 percent land area of China.
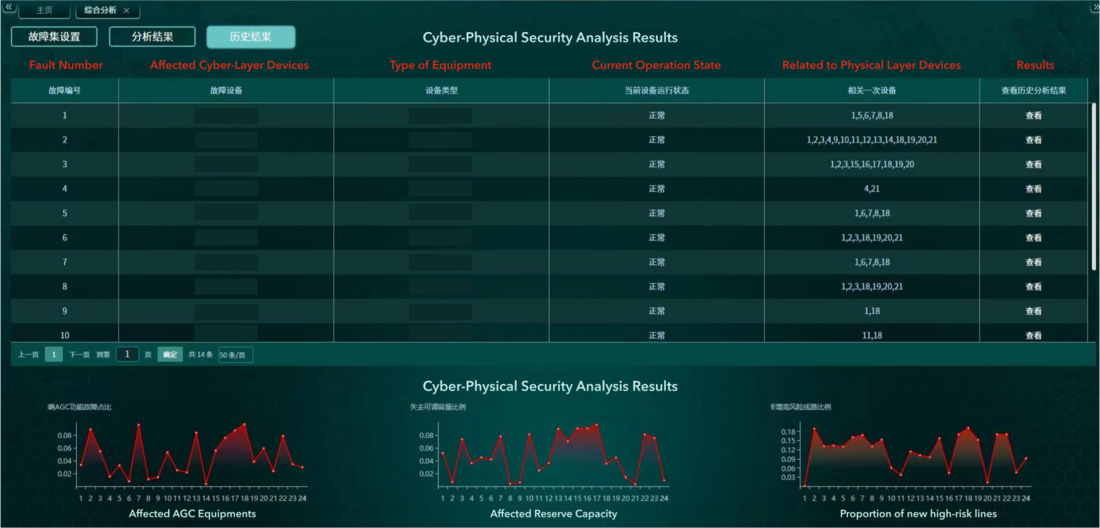
Figure 7 - N-1 cyber-physical security analysis function in the Cyber-Physical Monitoring and Control System (CPMCS)
Based on our CPS model for this real-world bulk power grid, the cyber-physical security analysis for its AGC system is performed with an N-1 communication failure scan based on the computation of information-energy flow and cyber-physical sensitivity method [6],[9], as shown in Fig. 7. Therefore, the impact of communication failures on the power system operation can be quantitively analyzed. This system extends the security analysis function of traditional power systems and supports modern power systems embedded with complex advanced information systems.
3. Application I: Resilient communication routing optimization under cyber-physical disturbances
3.1. Motivation
In a modern power system, various services are carried on OPGW (optical fibre composite overhead ground wire)-based communication networks. The optical fibres of an OPGW-based communication network are composite in the overhead lines of the power grid, and the topologies of these OPGW-based communication networks are, in most cases, in accordance with power grids, as shown in Fig. 8. Consequently, the strong coupling of these two networks may incur cyber-physical coupling failures in certain deteriorated situations, e.g., southern China’s 2008 ice disaster, which caused widespread disruptions of transmission lines and communication links.
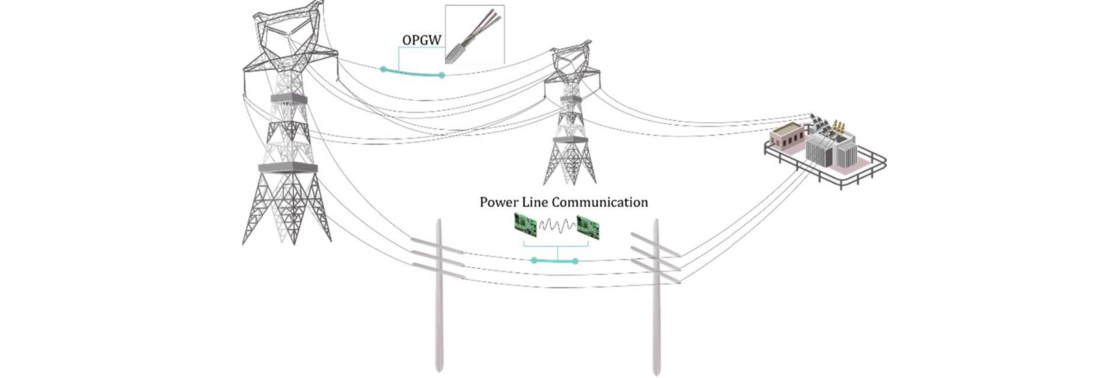
Figure 8 - Schematic of optical fiber composite overhead ground wire (OPGW) and power line communication (PLC) solutions
Despite the negative interaction effect of information flow and energy flow due to the in-depth interdependences of CPPSs, as shown in Fig 9, one can still be able to take the benefits from such interdependences. Compared with controlling the energy flow on the physical side, scheduling the information flow through the communication network on the cyber side is easy, efficient and economical. Therefore, to improve the resilience of a CPS in the face of cyber-physical coupling failures, we design a cyber-side routing mechanism that allocates critical information to reliable paths in [2], [7].
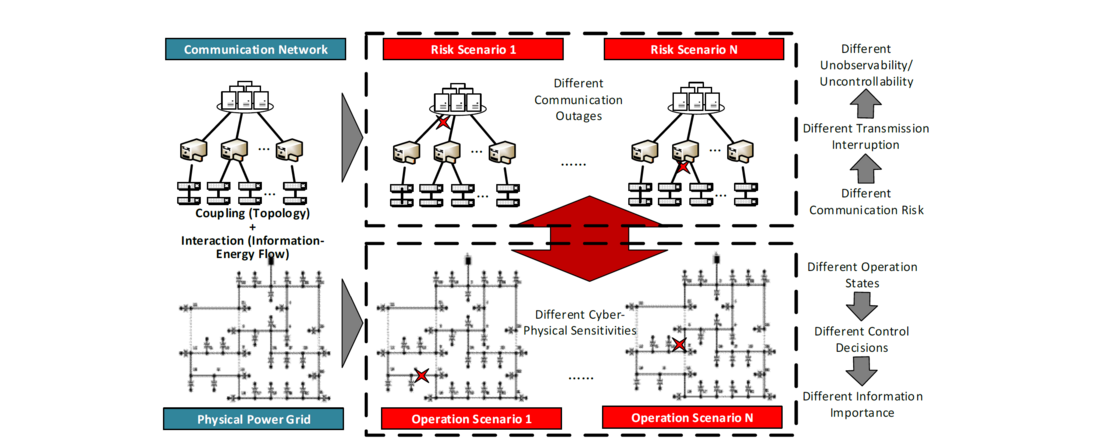
Figure 9 - Interaction effects of information flow and energy flow under different scenarios
3.2. Method and numerical test
A novel robust routing optimization model for the remedial control services of smart grids that considers cyber-physical interdependence is proposed in [2]. First, the importance of information flow is evaluation based on the information-energy flow model and cyber-physical sensitivity. To improve the resilience and survivability of smart grids during possible cyber-physical coupling failures, a CPS robust routing model (CPS-RRM) with a priority mechanism that allocates reliable paths to critical information flow considering cyber-physical uncertainties is proposed based on robust optimization. The routing optimization can schedule the main and alternate routing simultaneously.
By identifying the critical information flow in a specific operation state of power systems, the information flow of power flow correction control (PFCC) service can be adjusted adaptively against different communication risks, as shown in Fig 10, where the black solid line and the gray dotted line indicate the paths of the main and alternate routings, respectively, and the yellow nodes represent critical end nodes. Moreover, this method also takes into account the uncertainties in power systems including renewable generation fluctuations, load demand uncertainties and transmission line outages.
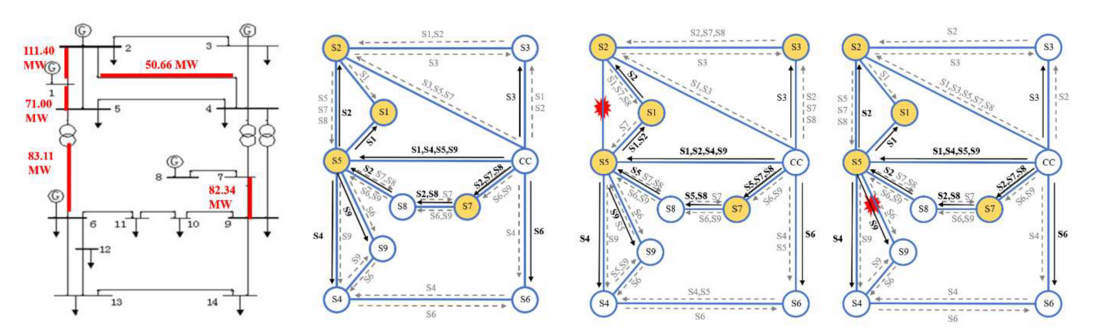
Figure 10 - Different communication routing schemes against different risk scenarios [2]
Considering the uncertainties of power fluctuation on the physical side and communication network failures on the cyber side, we defined the CPS uncertainty set with both cyber contingencies and power fluctuation. Monte Carlo simulations are carried out to compare the performance of CPS-RRM and the conventional shortest path routing model (SPRM) under the CPS uncertainty set. Up to 5000 scenarios are generated independently and randomly with power fluctuations on the physical side and “N-2” link outages of the high-risk area on the cyber side.
| CPS-RRM | SPRM | Deviation | |
|---|---|---|---|
Average | 24.0307 MW | 24.3897 MW | -1.47% |
Max | 44.9682 MW | 76.0788 MW | -40.89% |
It can be observed that the load shedding under the CPS-RRM communication routing strategy in these scenarios is apparently less than that of the SPRM, especially the maximum load shedding, which indicates that the proposed communication routing strategy can significantly enhance the resilience of power systems.
3.3. Deployment in real-world power grids
This method has also been further developed into a Cyber-Physical Risk Assessment and Management System (CPRAMS) platform deployed in Guangdong Province Power System in China, which is the province with the largest power generation. This platform first evaluates the importance of information flow according to its impact on the physical power system based on real-time operating data of the Guangdong Province Power System [6],[8]. Then, the main and alternate communication routing of remedial control services will be designed by the proposed CPS-RRM optimization model. For risk assessment, the load shedding under cyber-physical N-2 scan will be calculated based on the proposed information-energy flow model.
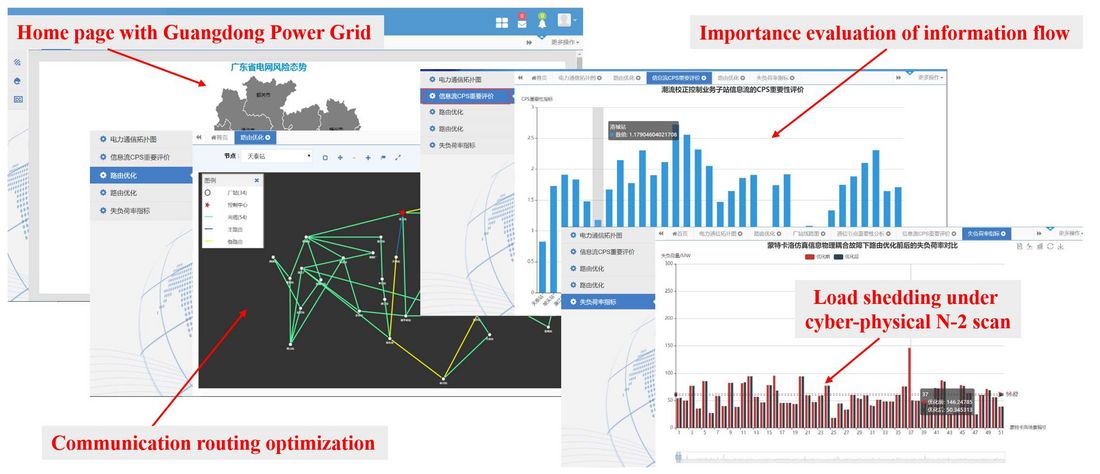
Figure 11 - Cyber-Physical Risk Assessment and Management System (CPRAMS) in Guangdong Power Grid.
Conventionally, the operators in Guangdong Power Grid design the routing strategy of remedial control service manually based on SPRM. By using our proposed CPS-RRM routing strategy, the loading shedding under cyber-physical uncertainties with both communication links and power transmission lines N-2 scan can reduce the loss of load by up to nearly 60% in Guangdong Power Grid. The results are compared in Table II, which also can be found in [2].
Case |
| CPS-RRM | SPRM | Deviation |
Guangdong Power Grid | Average | 26.8471 | 59.8233 | -55.12% |
Max | 118.1177 | 295.1122 | -59.98% |

4. Application II: Stability analysis and stability region of CPPSs with multiple time delays
4.1. Motivation
For a CPPS, disturbances or contingencies on the cyber side of an information system have significant impacts on the physical side. In particular, time delay or latency is among the most critical issues in information systems [3]. The time delay problem remains one of the main obstacles to the industrial implementation of wide-area control systems (WACSs) in bulk power systems and fully distributed control in microgrids. With the further development of digitalization, the delay effects on power systems will become more prominent [4].
Different from the research on algorithm stability and power systems stability, we focus on a more complicated issue, that is, CPS stability for modern power systems embedded with advanced information systems considering the time delay effect, as shown in Fig. 12.
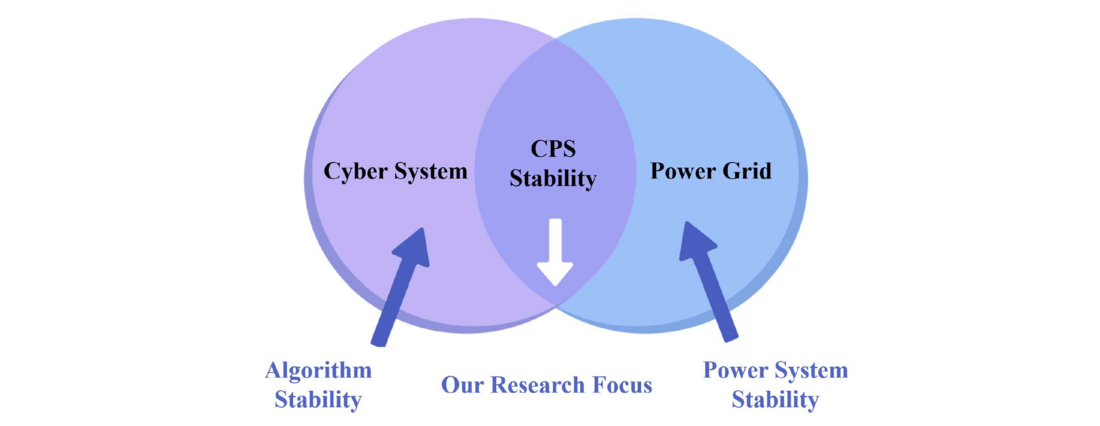
Figure 12 - Cyber-Physical System Stability
It is noteworthy that different from the traditional stability analysis of time-delayed power systems with decentralized controllers, this work [3],[4] deals with the stability analysis of CPPS with more complicated communication networks and heterogeneous delays. This work investigates the CPPS with consideration of multiple sources of time delay, both the local measurement and control execution delay and the communication delay from different controllers, as shown in Fig. 13.
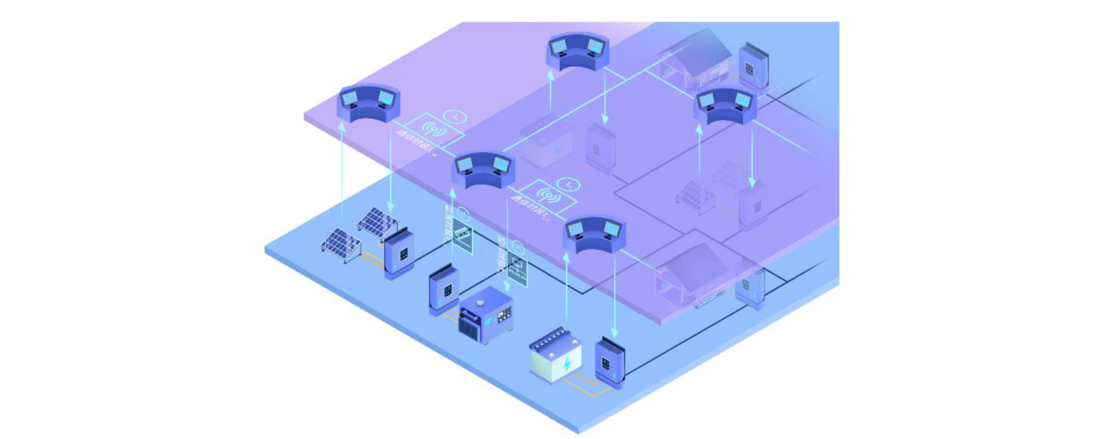
Figure 13 - A Cyber-Physical Power System with Multiple Time Delays [4]
4.2. Methods
To study the impacts of multiple sources of time delay on the stability of CPPSs, the proposed information-energy flow model in Section 2 is further developed into a dynamic information-energy flow model for CPPSs with heterogeneous time delays in all activities on the cyber side [3], as shown in Fig. 14.
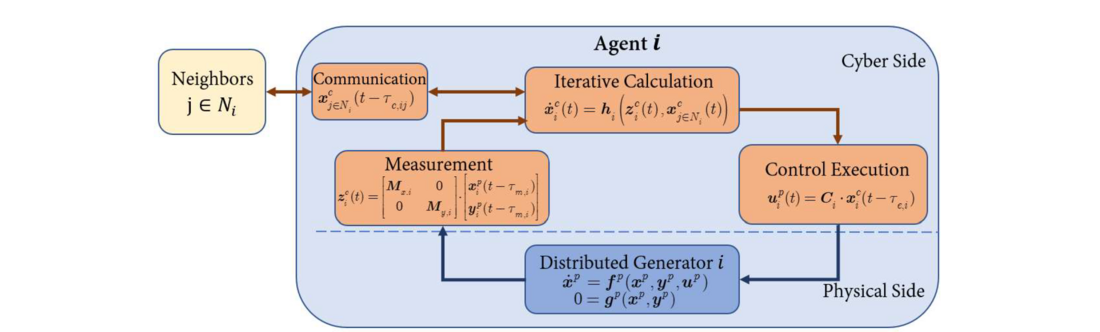
Figure 14 - A dynamic information-energy flow model for CPPSs with time delays [3]
Based on the above dynamic information-energy flow mode, a characteristic equation for time-delayed CPPS is established with multiple periodic transcendental terms induced by time delays. Such intractable equation has infinitely many solutions and cannot be solved directly. In addition, unlike the characteristic equation for a power system with a single-time delay local controller, which can be directly solved by the function transformation method.
Therefore, we propose a critical eigenvalue tracking algorithm for the stability analysis of time-delayed CPPS. As shown in the flow chart in Fig. 15, the algorithm considers the relationship between multiple sources of time delay in a DCPPS and can reduce the dimensionality of the multiple sources of time delay. The transcendental delay terms are replaced by constant terms at a certain delay direction. Moreover, by setting the proper delay interval according to the least common multiple of different delay ratios, the first marginally stable state caused by the increase in delay can be quickly located. Based on the proposed algorithm, the stability region of a time-delayed DCPPS with multiple sources of time delay can be efficiently and accurately obtained.
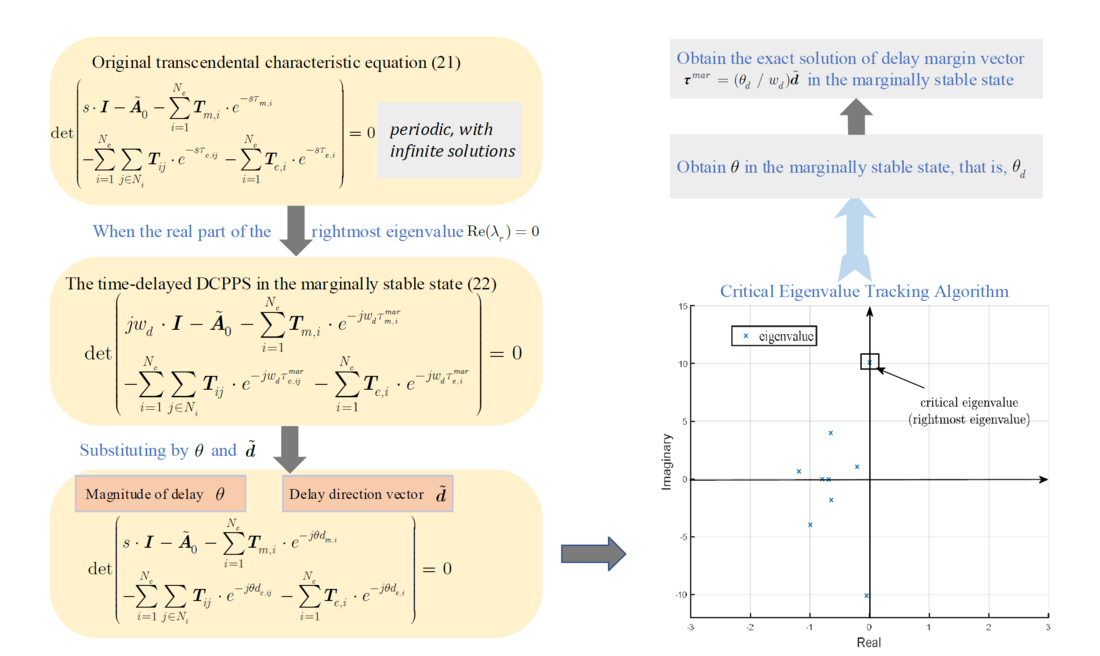
Figure 15 - Flow chart of the proposed critical eigenvalue tracking algorithm [3]
4.3. Case studies
For case studies, a 10.5 kV AC islanded microgrid system from a real-world 3-feeder 62-bus distribution network in Xiamen, China, is selected as a DCPPS and tested based on a fully distributed power dispatch method for frequency recovery, as shown in Fig. 16. On the physical side, two microturbines (MTs), one energy storage system operating as a VSM, and one photovoltaic (PV) under local P- droop frequency control are connected to the test microgrid through inverters.
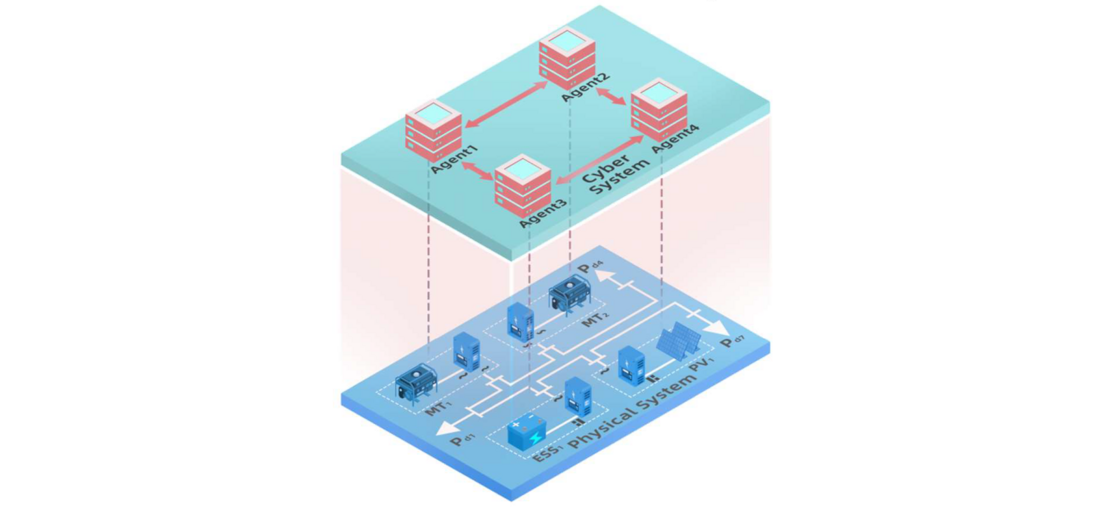
Figure 16 - A real-world 10.5 kV AC islanded microgrid with 4 DGs
Fig. 17(a) shows the stable region considering the local measurement delay and communication delay calculated by the proposed algorithm. The filled green region denotes the stable region, and the boundary is the stability margin in the marginally stable state. The stability of four representative points in Fig. 17(a) is analyzed based on the simulations by Simulink, as shown in Fig. 17(b). From the simulation results of points C and D, it can be observed that such points at the boundary of the stability region are in a marginally stable state, which also verifies the accuracy of our proposed model and algorithm.
By comparing points A and B, it can be observed that when measurement and communication delays exist, a shorter communication delay does not necessarily contribute to the stability of the system. The result indicates that the stability of a time-delayed CPPS with multiple time delays depends on not only the absolute value of the time delays but also the relative value and coordination of time delays. In some occasions, decreased delays do not necessarily have a positive impact on stability.
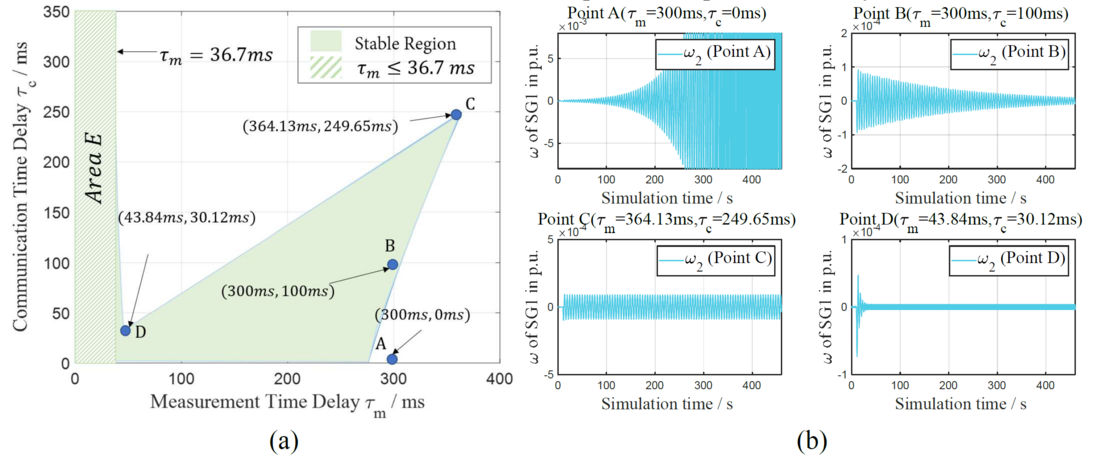
Figure 17 - Stability region and simulation results of the test microgrid under fully distributed frequency control considering time delays [3]
5. Application III: Stable synchronization period for CPPSs under non-ideal synchronous control
5.1. Motivation
The requirement for accurate time synchronization is extremely important for modern power systems embedded with advanced event-driven information systems on the cyber side. For instance, the IEEE 1588 protocol coexisting with the IEC 61850 standard is designed to guide accurate synchronous timing techniques in smart grids. It has become a basic consensus that an improper synchronous control period is harmful to the dynamics of the controlled power system and may lead to system instability. Therefore, it is critical to design a proper synchronization period or sampling period for the power grids’ control systems.
However, Simulation-based methods provide little theoretical insight into how synchronous control period influences the system stability. Thus, our work [5] provides a CPS model-based theoretical analysis of the impact of a synchronous control period on CPPS stability and can determine a stable synchronization period of control systems for CPPSs.
5.2. Methods
For real-world industrial clock-synchronization control systems, there is an inevitable asynchronous phenomenon due to the independent and random latency from the measurement on the cyber side to the control execution on the physical side of each controller, as shown in the left figure in Fig. 18. To take into account this asynchronous phenomenon, a general sampled-data control model for synchronized CPPS is proposed in [5], also as shown in Fig. 18. Then, the model is switched into a discrete state-space representative by discretizing according to the synchronization period T.
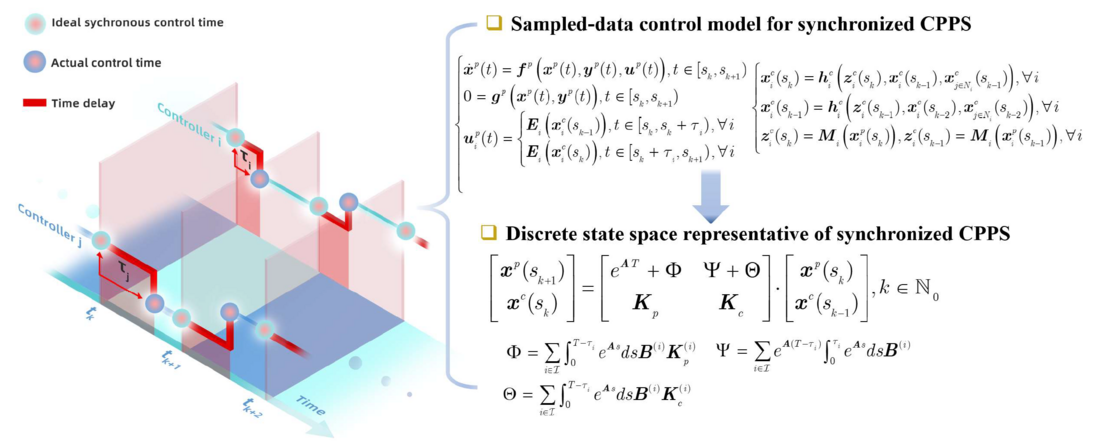
Figure 18 - Asynchronous phenomenon in real-world clock-synchronization information systems with multiple controllers and the related cyber-physical model [5]
Based on the proposed discrete-time CPS model, the stability criteria for studying the impact of synchronous control period on the stability of the synchronized CPS is proposed, as shown in Theorem 1 and Theorem 2 in Fig. 19. These stability criteria consider the asynchronous phenomenon of synchronized CPS under different delay conditions. Compared with Theorem 1, Theorem 2 uses switched Lyapunov functionals to solve the more practical scenario, that is, a system with random and independent delays in every control cycle for each controller. Although the time-domain method based on linear matrix inequality (LMI) is adopted in Theorem 2, it has also been proved in [5] that it has low conservation and computational complexity. Instead, the stability criterion of Theorem 1 based on spectral radius analysis is completely accurate without any conservation.

Figure 19 - (1) Left: Stability criteria for synchronous-control-based CPPS under asynchronous phenomenon; (2) Right: feasible stable control-period determination algorithm [5]
Then, based on the above stability criteria, a feasible stable control-period determination algorithm is proposed to calculate an interval of stable synchronization period for synchronized CPPS considering asynchronous phenomena, as shown in Algorithm 1 in Fig. 19.
5.3. Case studies
A 10.5-kV inverter-based AC microgrid from a real-world three-feeder 62-bus distribution network operating in an islanded mode is chosen as a test cyber-physical system, also as shown in Fig. 16. On the cyber side, a synchronous sub-gradient-based fully distributed frequency control algorithm was embedded. Notably, different from the continuous model in Section 4, in this section, the sensor of each distributed controller is time-driven by a clock-synchronization system; the iteration calculator and actuator are event-driven.
First, to verify the correctness of the proposed model and accuracy of the obtained stable synchronous control period, it is first assumed that the delays of all agents in the test microgrid are equivalent; that is, . Based on Theorem 1 and Algorithm 1 in Fig. 18, the obtained stable synchronous control period interval of the test system is within [12.4 ms; 284.5 ms]. Fig. 5 shows the spectral radius of the test system and Simulink-based simulation results of four key points (A-D).
It can be seen from these results that the simulated synchronous control periods of the system, T = 284 ms, T = 284.5 ms, and T = 285 ms, correspond, respectively, to the stable state, marginally stable state, and unstable state, which is consistent with the theoretical results obtained by Theorem 1.
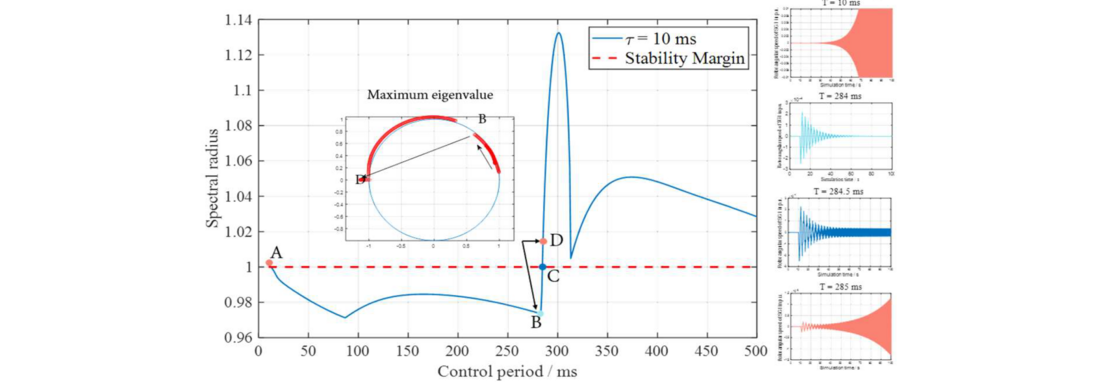
Figure 20 - Spectral radius of the system with 10 ms time delay and simulation results of points A-D [5]
It is also noteworthy that when the synchronous control period is too short (e.g., T = 10 ms at point A) the system may become unstable. This phenomenon can be explained by the theory of a sample-data control system. Owing to the overly fast synchronous control cycle, the system with a certain transient time constant cannot complete the entire state transition, and the control command from the next control cycle is superimposed on the system state, leading to system instability.
To better study the impacts of multiple time delays, it is assumed that the delays of MT1 and MT2 in the test system are equal to d1, and the delays of ESS1 and PV1 are equivalent to d2. As shown in Fig. 7(a)-(h), as the multiple time delays increase, the stable interval of synchronous control period for the system gradually shrinks. It can be seen from Fig. 7(a)-(e) that when d1, is shorter than 50 ms and d2 is in the range of [50, 65] ms, the system will be unstable under an 80-ms synchronous fully distributed control period. On the contrary, when d2 is within this range (even longer than 65 ms), the system can be stable, which illustrates not only that the absolute values will affect the stability of the system under a certain synchronous control period.
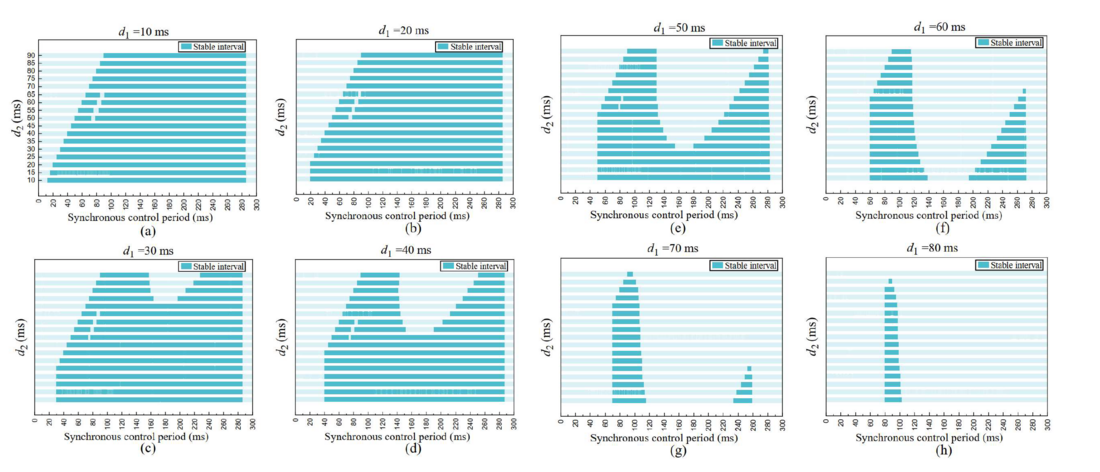
Figure 21 - Spectral radius of the system with 10 ms time delay and simulation results of points A-D [5]
Generally, the findings show that the synchronization period for the stability of CPPSs under the asynchronous phenomenon is determined not only by the absolute values but also by the coordination of multiple time delays. The results also show that the switching delays lead to a stricter stable interval. The proposed method can be used to guide the design of microgrids under fully distributed control.
6. Conclusion
The superposition of the vulnerability of cyber and physical spaces brings new challenges to the operation of modern power systems embedded with advanced information systems, that is cyber-physical power systems (CPPSs). This Ph.D. work proposes a hybrid information-energy flow model considering the in-depth interdependences of cyber and physical systems, which lays the foundation for integrated optimization and analysis of CPPSs considering the impacts of communication networks. For the resilience of CPPS under cyber-physical coupling uncertainties and malfunctions, an optimal robust communication routing strategy is proposed by allocating critical information flow to reliable links, which can reduce load loss in extreme scenarios. For the stability of CPPS under the impact of network latency, the time-delayed stable region of CPPS is obtained efficiently and accurately based on the proposed time-delayed dynamic information-energy flow model and critical eigenvalue tracking algorithm. For the inevitable asynchronous phenomenon of CPPS based on clock-synchronization control systems, the proper stable synchronous control period is determined by the proposed asynchronous event-driven CPS model and corresponding stability criterion.
This Ph.D. research work has been further developed into the Cyber-Physical Monitoring and Control Systems (CPMCS) Platform and Cyber-Physical Risk Assessment and Management System (CPRAMS) Platform that already embedded in several real-world bulk power systems, supporting the resilient operation of power systems via integrated risk analysis and prevention control.
References
- L. Xu, Q. Guo, Y. Sheng, S.M. Muyeen and H. Sun, “On the resilience of modern power systems: A comprehensive review from the cyber-physical perspective,” Renewable and Sustainable Energy Reviews, 2021, 152: 111642.
- L. Xu, Q. Guo, T. Yang and H. Sun, “Robust routing optimization for smart grids considering cyber-physical interdependence,” IEEE Transactions on Smart Grid, 2019, 10(5): 5620-5629.
- L. Xu, Q. Guo, Z. Wang and H. Sun, “Modeling of time-delayed distributed cyber-physical power systems for small-signal stability analysis,” IEEE Transactions on Smart Grid, 2021, 12(4): 3425-3437.
- L. Xu, Q. Guo, G. He and H. Sun, “Novel properties of heterogeneous delay in inverter-based cyber–physical microgrids under fully distributed control,” Applied Energy, 2022, 306: 118102.
- L. Xu, Q. Guo, G. He and H. Sun, “The impact of synchronous distributed control period on inverter-based cyber–physical microgrids stability with time delay,” Applied Energy, 2021, 301: 117440.
- L. Xu, Q. Guo, H. Sun and Z. Su, “A routing optimization model for EMS of power systems considering cyber-physical interdependence,” 2017 IEEE Conference on Energy Internet and Energy System Integration. Beijing, 2017: 1-5.
- Q. Guo, S. Xin, L. Xu and H. Sun, “EMS communication routings’ optimisation to enhance power system security considering cyber-physical interdependence,”. IET Cyber-Physical Systems: Theory & Applications, 2018, 3(1): 44-53.
- X. Liu, L. Xu, Q. Guo, T. Sheng, T. Yang, Y. Huang and Z. Wu, “Sensitivity-based critical measurement identification of state estimation: From a CPS perspective,” 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 2018: 1-6.
- Z. Su, S. Xin, L. Xu, Z. Shi, Q. Guo and H. Sun, “A compensation method based assessment of cyber contingency for cyber-physical power systems,” 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, USA, 2018: 1-5
Biography

Luo Xu received his B.S. degree from the School of Electrical Engineering, Wuhan University, China, in 2017, and the Ph.D. degree from the Department of Electrical Engineering, Tsinghua University, China in 2022. He is currently a Postdoctoral Associate in Department of Civil and Environmental Engineering, Princeton University, USA. His current research interests include resilience and stability analysis of cyber-physical power systems, and environmental impact on power systems.
He is a member of CIGRE, CIGRE NGN and IEEE. He serves as the Secretary of CIGRE Working Group D2.56 on “Interdependence and Security of Cyber-Physical Power System”, the member of IEEE Task Force on “Cyber-Physical Interdependence for Power System Operation and Control”. He is also a reviewer for several high-reputation journals such as IEEE Transactions on Smart Grid and IEEE Transactions on Power Systems. He was a recipient of the IET Premium Awards in 2019 and the Best Conference Paper Award from the IEEE Conference on Energy Internet and Energy System Integration in 2017, and the Outstanding Reviewer for IEEE Transactions on Power Systems in 2020.

Qinglai Guo is currently tenured Professor with the Department of Electrical Engineering, Tsinghua University where he received his B.S. degree and PhD degree in 2000 and 2005, respectively. He is now an IET Fellow, IEEE senior member and a CIGRE member, and is involved in 5 workgroups of these organizations. Now he is TCPC of Energy Internet Coordinating Committee of IEEE PES, the co-chair of IEEE PES Work Group on “Energy Internet”, IEEE PES Task Force on “Cyber-Physical Interdependence for Power System Operation and Control”, and IEEE PES Task Force on “Voltage Control for Smart Grid”. He is an editorial member of IEEE Transactions on Power Systems, Renewable & Sustainable Energy Reviews, IEEE Transactions on Smart Grid. His special fields of interest include smart grids, cyber-physical systems and electrical power control centre applications.
