Applying a physics-consistent general power theory to practical electricity systems with unbalance and periodic waveform distortion – Part 1: Implementation, testing, application to DG
Authors
C. T. GAUNT, H. K. CHISEPO – Dept. of Electrical Engineering, University of Cape Town, South Africa
M. MALENGRET – MLT Drives, Cape Town, South Africa

Summary
Reactive and apparent power are not power or energy. Their present definitions and computation classify them as components of power added geometrically, but this is inconsistent with the laws of physics of circuits and cannot represent accurately the performance of most practical electrical power systems. The problem lies in the concept model of reactive power orthogonal to power in a right-angled PQS triangle.
A novel alternative general power theory (GPT) formulated through linear algebra can directly identify the optimal currents at a point of connection for minimum delivery loss for the same power. The novel measurement (or concept) model represents an apparatus or complex power system with all the influencing quantities of any number of wires, unbalance, and harmonic distortion. Compensation by power electronic converters is possible.
Part 1 of these two comprehensive papers describes, with examples, the GPT’s measurement of useful power parameters, interprets and compares them with some other theories, and describes the testing of the new theory. An application to inverter control for distributed generation is examined with a numerical example. Applications to voltage stability in the presence of distortion by GICs, and to metering and electricity tariffs that challenge accepted practice are in Part 2.
These papers will likely interest utilities engaged in generation, transmission and distribution, market operators, manufacturers, regulators, researchers, and academics.
Keywords
Active distribution network – Apparent power – Distortion – Inverter-based generators – Power electronics– Power factor – Reactive power –Unbalance – Voltage control1. Introduction
Various concept models, theories, and definitions of electric power components have been proposed since 1890. Different ways of defining and measuring parameters with the same name, such as apparent or reactive power, produce results that are difficult to interpret in physical terms. Despite unsettling shortcomings, the theories survive and are taught to successive generations of engineers.
Why are measurements made at all? Mostly, a parameter is measured so that it can control, or be controlled, or be a basis for costing or comparison. Thus, power parameters are used technically to improve system efficiency and stability, for regulating tariffs and power quality, and financially to determine fair prices for energy, capacity, and ancillary services. As the same measurements may be used for different purposes, it is desirable that they consistently represent real power system performance.
A practical power system comprises one or more sources, a delivery system, and one or more loads. It operates at dc or ac, or as one modulated by the other, and with waveforms distorted by harmonics. Practical systems are unbalanced with different impedances, voltages, and currents in the various wires.
Fundamentally, only voltages and currents are sensed in a system at points of connection (PoC) or common coupling (PCC). The laws and principles of physics, however, allow several relationships to be defined by combination.
Early experimenters addressed how the power delivery of ac systems differed from dc systems. The interest was (and still is) in the inter-relationships between currents, voltages and voltage drop, power, and energy flow and dissipation by resistive heating in the supply system. The product of ac voltage and current gave the power in resistors, but not in inductors. Terms like wattless power and apparent power [1] were introduced to signify and quantify the differences, but these were not physical quantities of classical power. A century of debate followed the early proposals – and continues.
This paper introduces a general power theory (GPT) for practical systems with any number of wires. It is based on a novel measurement model that includes all the influencing quantities of unbalance and distortion, and it is suitable for steady-state measurement and control. With only physics consistent terms of voltage, current, impedance, power, and energy, based on local measurements of voltage and current, an appropriate mathematical approach was used to derive useful physical parameters.
The wide applicability of the GPT is illustrated in Fig. 1. At the meter, the 3-wire system could be from a centre-tapped single-phase ac supply, two phases and neutral of a 3-phase system, an open-delta 3-phase supply, a split dc system, or various other configurations not distinguishable until measurements are made. The GPT applies equally to all of them.
The application and some implications of the novel theory are explored. An unexpected property of the GPT is that it cannot accommodate any forms of reactive and non-active power that are not power and are operational measurements without interpretation in terms of physics. This is not mere terminology – it is an evidence-based way of thinking scientifically about power system circuits.
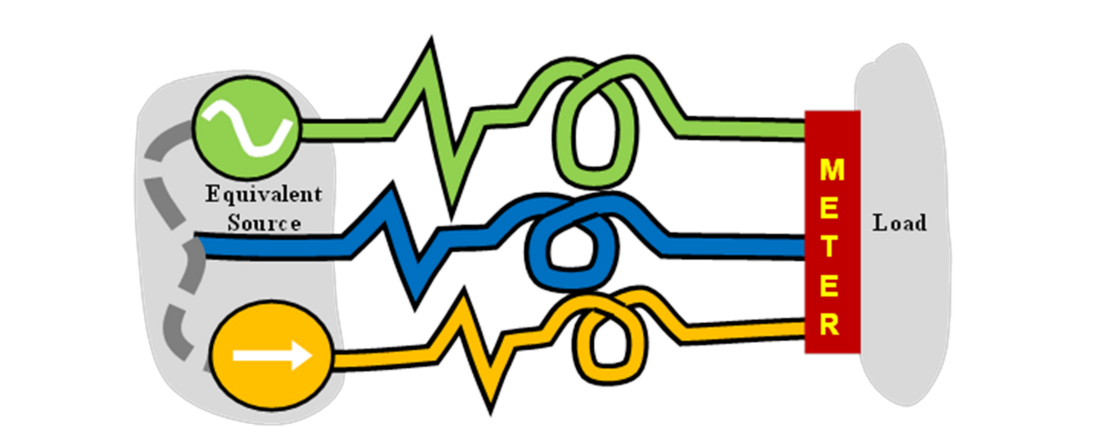
Figure 1 – Any 3-wire unbalanced, waveform-distorted system supplying power to a load
Questioning notions of reactive power and redefining apparent power challenge traditional power engineering knowledge. However, the GPT offers potential benefits in terms of addressing measurement issues, system design, decision-making, policy formulation, and fair electricity pricing. Several research papers explore innovative applications and outcomes resulting from alternative approaches like GPT.
Hereafter, section 2 reviews significant developing themes relevant to power theory. Section 3 does not repeat the already-published GPT derivation, and the proof that the compensation produces the optimal (minimum) delivery loss [2]; instead, it applies the GPT to some simple examples and interprets key results. Section 4 describes its testing. In section 5 the GPT is compared with conventional approaches to distributed generation control. In Part 2, other practical applications and implications are examined in Section 6 (voltage stability with GICs), 7 (meters and tariffs), 8 (teaching, research, and policy), and 9 (definitions for power terms). Section 10 offers some conclusions.
2. Review of developing themes
2.1. Technology Changes
Four major technology trends are combining to change modern power systems from those of the 20th century. Environmental concerns drive greater use of renewable energy that is variable and requires backup from storage or dispatchable energy sources. Second, many new sources are distributed closer to the edges of power systems, where distortion and phase unbalance are greatest. Third, power electronics technology with fast current control is changing the character of loads, inverter-based sources and storage, and even the wired system. Fourth, digital techniques have replaced most analogue measurement and control, presenting new opportunities and some problems.
These four trends are often represented as characteristics of smart grids, but they apply generally to electricity supply systems, changing the tasks of planners and operators and giving them the technologies to meet the systems’ needs.
2.2. Models of Apparatus and Power Systems
An apparatus, as distinct from a power system, is an assembly of circuit elements connected to the system at a PoC. It can be a load, a source, or a whole network of loads and sources. An apparatus has a set of ideal source voltages at its terminals. If the elements change or are re-arranged, the currents will too, without affecting the voltages. Changing the set of voltages causes currents to change according to the voltage sensitivity of the apparatus, often referred to as impedance, current or power models of a load but usually a mix of these responses.
Most power theories define power components for an apparatus, neglecting the effects of power delivery impedances on the voltages at the PoC. Some define a power system with resistances in the phase wires (usually assumed equal) and a neutral wire (usually with equal resistance or none). A few include resistance and inductance. Most theories that include delivery resistance or inductance assume known balanced and undistorted equivalent source voltages, without practical access to measure them.
2.3. Prior Power Theories
Past power theories have been reviewed in many papers. Our initial derivation of the GPT in the time domain for a three-phase system was published in 2008 [3]. The approach was extended to systems with any m-wires a few years later [4] [5], [6]. Those early papers included reviews of the theories of Fryze, Depenbrock, Buchholtz, Akaji, Willems, Ferrero, Nabae, Rossetto, Peng, Dai, Salmerón, Filipski, Czarnecki, Jeon, Morsi, Emanuel, Mayordona, Mishra, Montero, Ustariz, Atefi, and their co-authors. The discussion and many references are not repeated here; the interested reader is referred to the original papers. Some of these and others have been identified in a more recent survey of time domain theories [7].
Our time domain theory was unable to accommodate frequency dependent impedances such as represented by skin effect and reactance at harmonic frequencies, so we extended the GPT into the frequency domain [2], which also corrected some flaws of the time domain GPT, notably its formulation of reactive power. That paper included reviews (also not repeated here) of more recent developments of the p-q, conservative power and current physical components theories, and others, by Czarnecki, Burgos-Mellado, Schäffer, Montoya, Moriano, Monteiro, Dey, Mikulović, Jeon, Bhattarai, Lev-Ari, and their co-authors.
Looking back much further, in 1893 Kennelly used the term impedance factor and introduced an impedance triangle, leading to discussion by Steinmetz of the effect of the whole system on the voltage drop in power delivery [8]. In 1910 Kennelly extended the impedance triangle to power and energy [9], shown in part in Fig. 2.
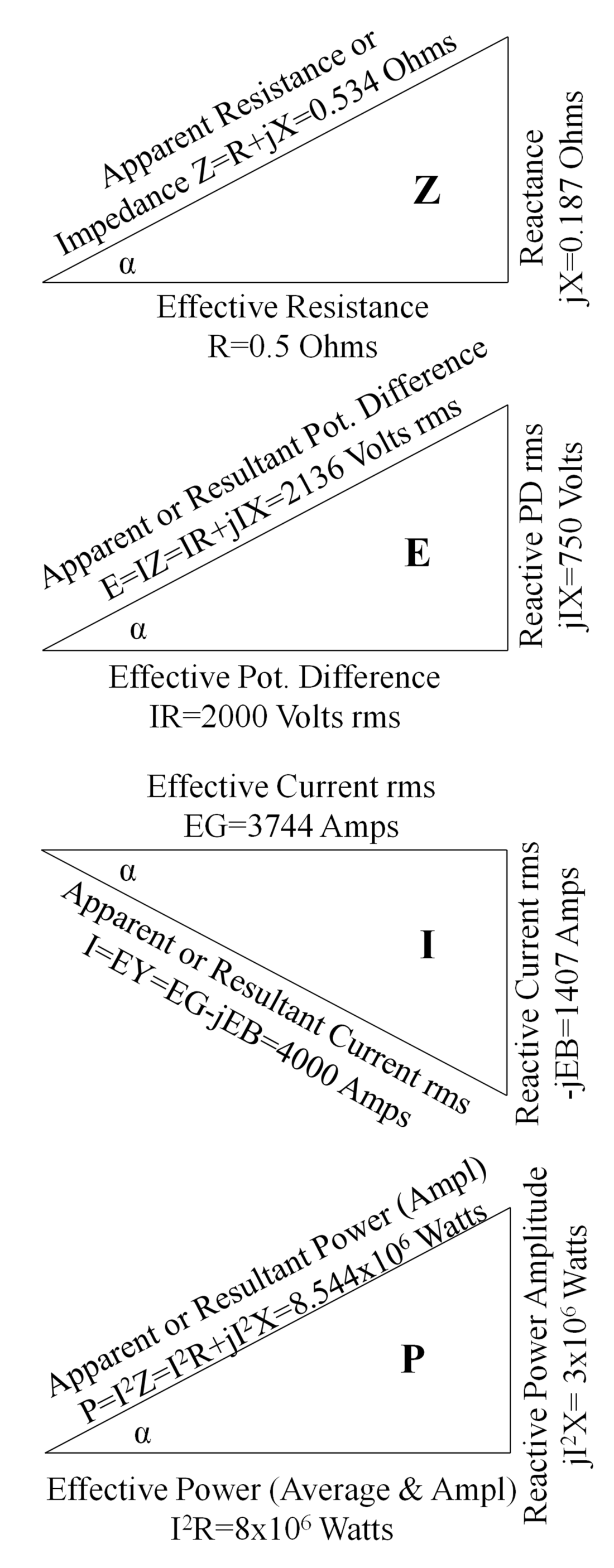
Figure 2 – The origin of the power triangle: some of Kennelly’s stationary vector diagrams – single-phase impedance Z, potential difference E, current I, and power P in an alternating current circuit [9]. Power is a scalar quantity, and the concept model of the power vector triangle is incompatible with physics
In time, the many variables affecting power theory introduced such complexity that papers and discussions tended to focus on only a limited range of them. By 1920 it was “desirable to separate the effects of phase displacement, unbalance and wave form since the causes and remedies for each are quite distinct” [10]. Generally, the segregated approach has continued until the present, although we know now that separation introduces limitations. Beyond Steinmetz’ discussion [8], the complex relationship between the displacement angles at the source and load was not recognized by many, or neglected, even though the definition of unity power factor at the load did not achieve the minimum loss in power delivery [11].
When influence quantities (defined at IEV 311-06-01) [12] are excluded from a model and protocol, or contain invalidating assumptions, the uncertainty of a model-defined measurement’s representation of the physical behaviour of the system is undefined and cannot be known. Most power theories and most standards (including DIN [13], IEEE [14], and others) omit source impedance from the definitions of apparent power, reactive power, and power factor, so significant influencing quantities are neglected. Without referring to the practical source and line capacity or the avoidable loss (IEV 691-11-16) in the delivery system, utility tariffs include non-physical quantities with a unit of VA (IEV 691-05-06), and charges for power factor or reactive power (IEV 691-09-06).
Non-physical operational definitions and omission of influencing quantities introduce inconsistencies and ambiguity into interpreting measurement outputs. For example, multiple definitions of apparent power [14] and methods of measuring reactive power [15] lead to practical problems in billing customers [16], and waveform distortion may lead to smart meters displaying reverse power flow even in the absence of behind-the-meter generation [17]. Filtering the input signals removes the distortion from a measurement, but also any information about the effects of distortion.
At the same time, the objective of effective compensation leads to various approaches to deriving the non-active components of apparent power for a variety of system topologies [18], [19], [20], [21]. Most researchers assume balanced source impedances and/or treat the voltage at a load’s PoC as constant, though a few do not [22], [23], [24].
In summary, this review suggests (i) power electronics and digital techniques are changing the performance of power systems, (ii) system models with assumptions violated in practice by unbalance and distortion could be improved with more representative models based on parameters observable from the PoC, (iii) definitions of a load or source as an apparatus connected to constant voltage terminals might have uses but ignore power dissipated in delivery, and (iv) many mathematical definitions of non-active and apparent power and power factor are inconsistent with each other.
3. GPT for measurement and control
The novel concept of the GPT is that the transport of electric power in a multi-wire, multi-frequency network is shared by each wire and its frequency components. The power at a PoC over a time interval can be transmitted by the delivery system in infinite combinations but only one combination of wire- and frequency-components of current will transport the same energy with minimum loss. The uniqueness of the optimum combination (minimum loss for the power delivered) in a system with M-wires and H+1 frequencies is supported by a mathematical proof based on the orthogonality property of frequency components over a specific time interval, Kirchhoff’s laws, and the conservation of energy [2].
Therefore, only one current vector IA exists, consisting of a unique set of M x (H+1) optimal line current components IA m,h that deliver the power PPoC at the PoC with minimal loss, and is given by:
(1)
where: is a single real value constant, (2)
(3)
with +/- depending on the direction of total power flow,
(4)
(5)
and ' signifies resistance weighting by an array R based on the Thévenin resistances, a square M x M matrix with the M x (H+1) resistance elements of the delivery system, where the diagonal vector is and all other elements of the square matrix are zero. This approach identifies the minimum loss in the delivery system as
and the optimum power at the Thévenin point
.
Using one general physical model, the GPT defines the power parameters associated with a load, source or other network connected to a PoC. The same formulation is valid for systems with any number of wires of possibly unequal impedances, ac and dc, possibly unbalanced voltages and currents, and with waveforms distorted by harmonics.
The GPT is essentially a measurement process. But when applied to a compensator or inverter, the hardware cost of a GPT-controller is negligible and produces benefits from potentially achieving minimum delivery losses throughout the life of the system.
These advantages are constrained, however, by the assumption of steady-state conditions in which the frequency, load current and Thévenin equivalent parameters of the past one or several cycles will hold for the next cycles. Small variations of load or frequency can be accommodated in practice with a short delay when the conditions change. When the power frequency deviates too far or too quickly from acceptable limits, such as during a system fault, control for optimum energy delivery needs to be suspended and an alternative control approach adopted. Approaches to detecting transient system incidents and resuming GPT control are beyond the scope of this paper.
The application of the GPT is first illustrated using a simple example of the system of Fig. 1. It is based on a 3-phase 4-wire system with only fundamental frequency, in which an open circuit in one phase leaves the extremely unbalanced 3-wire supply shown in Fig. 3.
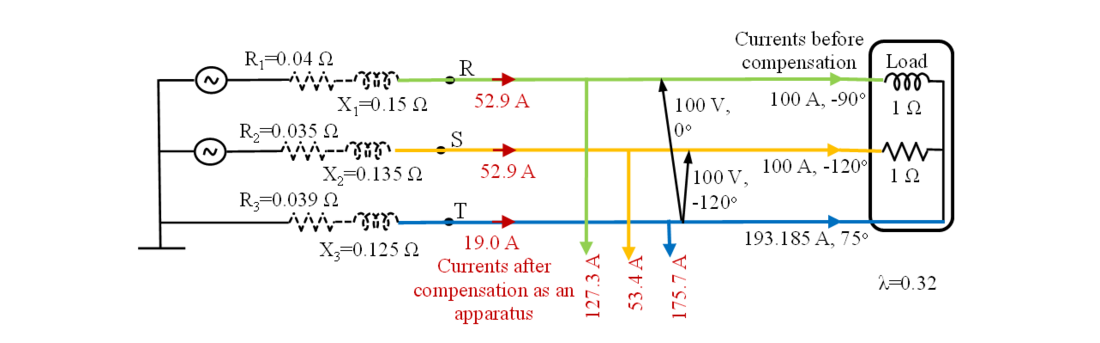
Figure 3 – Form and values of a 60 Hz 3-wire supply with a missing phase. The voltage measurement reference wire T is the neutral wire. The dashed source impedances are not in the original problem
The problem was posed [25] for only fundamental frequency and analysed using the Current Physical Components (CPC) approach. A second paper [18] calculated the compensation that draws only active current from the supply terminals. The case was presented as an apparatus, so for this example of GPT application an arbitrary small unbalance is added to the supply impedance. Extended versions of the problem are discussed in sections 4 (with harmonic components) and 7 (showing the missing phase of a 4-wire supply in Fig. 17). Three less extreme cases of unbalance using different examples were presented in [2].
The algebra of the GPT defines the same calculations processed repetitively for the number of wires and harmonic components. A spreadsheet offers an easy way to illustrate the simple calculation steps. It also facilitates translation into embedded controllers, simulations, and software languages. The key formulas of the spreadsheet, listed in [2], can be extended to include as many wires and harmonics as needed.
The implementation of the GPT can be thought of as having three steps: inputs, measurement, and control. These are described in sections 3.1 to 3.3.
3.1. Input parameters at the PoC
3.1.1 Voltages and currents
The first step in making a measurement is to sample the voltages and currents in each wire at the PoC. All voltages are measured from any common physical reference, usually one wire. Simultaneous samples of voltages and currents in each wire are taken at regular intervals and time-stamped.
The voltages and currents in dc systems are constant magnitudes in each of the M wires of a multi-wire system.
Distorted periodic waveforms of ac voltages and currents can be represented mathematically by the sum of weighted sinusoids, decomposed by Fourier analysis. Termed the fundamental and harmonic frequencies and possibly with a dc component (h0), these are not separate voltages and currents, but are components consistent with the Principle of Superposition. The cycle of interest may be one or several cycles at the fundamental power frequency or even a week, with periodic distortion represented as harmonics. Many sources give information about frequency measurement and Fourier analysis of sampled distorted waveforms.
Superposition allows the three wires of Fig. 1 to be modelled as an equivalent circuit of the load at the PoC with a sub-circuit for each frequency component. In the first example, the system contains only fundamental frequency.
The voltages and currents are vectors. As with many approaches, one voltage is defined as an angle reference and the angles of all other vectors are related to it. Currents into the apparatus are defined as positive. Scalar power into a load is positive, and out from a source is negative. The GPT is consistent for loads and sources.
For an M-wire system with (H+1) frequency components, the Fourier transform of the sampled measurements gives two M x (H+1) dimensional complex rms (CRMS) vectors U and IS. For the GPT, the voltages and currents U and IS are expressed as CRMS values for each wire and frequency component: x(t) = Asin(ωt + α) where A=amplitude, ω=frequency and α= phase angle. This is also referred to as the exponential form of the Fourier rms components for each wire, Ae jω(h)α, where h is the harmonic order. Several papers describe and use the CRMS representation of voltages and currents [18], [24], [25], [26], [27].
Table I shows the input parameters (CRMS voltages and currents, and equivalent impedances) for the GPT calculation of the system example of Fig. 3.
The voltages and currents give the arithmetic power at the PoC – see section 3.2.3.
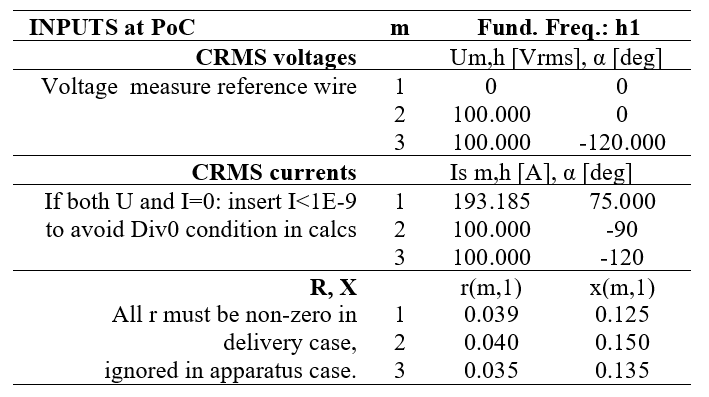
Table I - GPT input values for Figure 3
3.1.2 Equivalent source impedances
The widely used Helmholtz-Thévenin equivalent circuit of a system observable at a PoC is powerful because it incorporates unbalance in the impedances or the electrical distances to sources and loads, and harmonic disturbance from nearby sources.
The equivalent circuit impedances change when the supply system reconfigures, such as by line or capacitor switching and as loads change. Measurements on a low voltage network show the profile of the impedances follows a daily pattern [28] as loads add to the system demand and generators respond to supply it. The daily pattern may become less predictable as the penetration of wind DG increases.
There are many approaches to measuring the equivalent circuit impedances, including passive monitoring of network changes, active probing with a measurement instrument or by disturbing an existing compensator or inverter, and from PMU measurements. They can be derived also by a network reduction of a system model established by state estimation, or by disturbing a model by probing with extra load. Since the Thévenin theorem is based on small disturbances, the parameters differ from the transient and sub-transient source impedances of faults. The frequency range of current and voltage transducers affects the accuracy of practical measurements of harmonic impedances.
For applying the GPT, the equivalent impedances for all frequencies of relevance can be derived using the most suitable of the above approaches. The values of resistance rm,h and reactance xm,h define all M x (H+1) lines of the equivalent circuit to the PoC. These derivations are usually less uncertain than the estimated values of impedances used in many equations in power system analysis, and better than neglecting the source impedance entirely.
For an apparatus, no source impedance exists. An apparatus is defined only by its internal component impedances and the currents drawn for any set of terminal voltages. The apparatus case is described in section 3.4.
3.2 GPT calculation of power terms
3.2.1 Source voltages referred to original measurement reference
Using Ohm’s law, the voltages across the impedances of each of the M x (H+1) Thévenin lines are calculated and added to the voltages measured at the PoC to give the source voltages from the reference point at the PoC.
In simple terms, this takes the form: VTh = VPoC + ZlineIPoC. In linear algebra, the currents and voltages measured at the PoC form row vectors IS and U each consisting of the M x (H+1) CRMS values. Then, the voltage components at the equivalent source are where
for m = 1 to M and h = 0 to H, giving the M x (H+1) Thévenin complex voltage vectors VTh.
3.2.2 Source voltages referred to a null point
A distinct null reference point is needed at the equivalent source for each frequency component to keep the mathematics consistent with Kirchhoff’s voltage law. For each harmonic order h, there is a superposed Thévenin equivalent circuit with an offset between the reference point at the PoC and the equivalent source, and a reference offset vector of the form for each wire m. For each subsystem, VTh(null) is calculated by subtracting the respective eref,h offsets from VTh m,h, and gives
where the dash ' indicates a resistance-weighted value.
The offset vector is derived using the Gramm-Schmidt method in linear algebra, and the algebraic formulae maintain the structure of the CRMS values. (The process is described in equations (8), (18), (23), (26) and (27) and appendix of the GPT derivation [2] and all calculations are arithmetic.)
The calculated source voltages and reference point are shown in Table II.

Table II - Calculation of source voltages and Thévenin point null reference for Figure 3
3.2.3 Calculating P, APSYS and PFSYS
The calculated GPT power parameters associated with the load, source or network connected to the PoC of a practical power system are illustrated in Table III. (In section 4.1 Table VI, these GPT power measurements of APSYS and PFSYS are compared with those of Bhattarai.).

Table III - Power parameters for Figure 3
The current in a wire depends on the currents in all other wires, and the voltages and currents of the superposed equivalent circuits are related vectorially. However, the scalar power at the PoC and source cannot be attributed to a single wire or phase but given only as values for the whole system. (This is consistent with power measurement as the product of i(t) and v(t) such that the measurement depends on the voltage reference and every current-carrying wire.) Therefore, power terms are calculated for each frequency subsystem and then added to find the system total.
Having identified all currents at the PoC and all source voltages with respect to a null reference point consistent with Kirchhoff’s voltage law, the power at the source and the loss in the delivery system can be calculated. All power quantities are ‘real’ average power and have the unit of power W, and they are compatible in arithmetic calculations, including in dimensionless ratios. The significant power quantities include:
- The power PPoC delivered to the PoC is the inner product of vectors U and I. Expressed in CRMS form, the power of the M wires in each harmonic subsystem is
, and summed for the system PPoC = P0+P1+P2+…+PH. All GPT power parameters are associated with this PPoC.
- VPoC and PPoC are defined conventionally, but VTh and PTh at the Thévenin source are also needed for the GPT measurement of other power parameters related to PPoC.
- The power loss dissipated by the currents in the wire resistances is
, which is recognisable as the common expression I2R. The set of resistance-weighted current components IA' causing the minimum loss dissipation in the delivery system is given by the solution (6) of the quadratic equation (3) of the power PPoC and the norm of the Thévenin source resistance-weighted voltage, ||V'Th(null)|| of (5). The minimum delivery loss by implementing compensation is given by
where:
(6)
- The power sent out from the Thévenin source before compensation is
and the minimum power needed from the Thévenin source after compensation is
.
- From all sets of currents that dissipate the loss
,
can be defined as the optimally distributed set, giving
as the maximum power that could be sent out from the Thévenin equivalent source for the original loss. APSYS is real power in the physical sense and the units are Watts.
- The PFSYS is a dimensionless ratio of the loss without compensation and the minimum delivery loss for the same PPoC: √||IA'||2/||IS'||2. It is the same ratio as ||IA'||/||IS'|| and
PTh min/APSYS. It is an index of the relative efficiency of delivery. Being the ratio of powers at the source, “unity power factor” PFSYS =1 is the optimum relative efficiency for a given total active (or average) power transmitted from a source” [2]. The PFSYS is not the overall efficiency as defined by (loss) / (PPoC + loss).
The GPT does not depend on compensation; it measures actual power quantities associated with the PoC load as it is.
3.3 Active current distribution
A common proportionality factor (2) for the active current is used to calculate the optimal components of IA. Then the new voltages at the PoC are given by Ohm’s law, and the compensating current components IC by subtraction of IA from the uncompensated original IS. The results are shown in Table IV. Clearly, the active current components are not necessarily balanced.
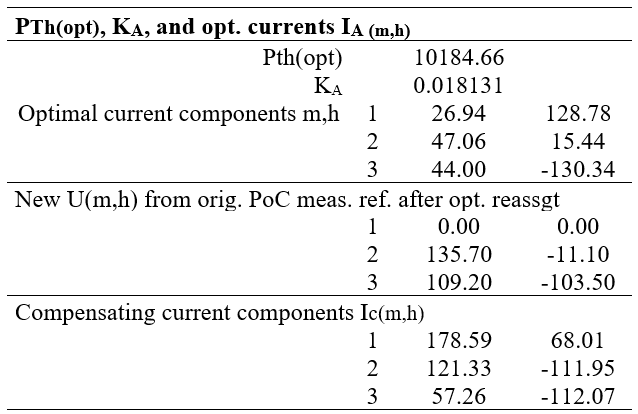
Table IV - Calculation of compensator currents for Figure 3
3.4 Simplification for an apparatus
For an apparatus with no source impedance, all terms in the GPT equations containing equivalent source impedances are modified by making the impedance values zero. A null reference point for the measured PoC voltages is needed to comply with Kirchhoff’s voltage law. The offset vector at the PoC is defined simply by the voltages, without resistance weighting, so this simplified form gives the same PPoC, while APAPP and PFAPP no longer have units of real power:
APAPP = ||Is|| ||Vnull|| (not resistance weighted, units VA)
PFAPP = PPoC/APAPP (not dimensionless but W/VA).
Measurements and compensation currents in the apparatus case adapting the GPT-based approach with zero delivery impedance are shown in Table V.
The GPT-based apparatus case for Fig. 3 gives results consistent with the CPC approach [18], [25] for this 3-wire example. The null point offset voltages correspond to those derived using symmetrical components [25]. The PFAPP is higher than for the same load in a delivery system, shown in Table III, because the estimate of APAPP is lower.
The term APAPP is not power and PFAPP cannot represent losses incurred in delivering power to the apparatus. Following Kennelly [8], PFAPP can be viewed as an equivalent impedance factor, IF=R/Z, of the apparatus for the set of voltages at its terminals. The compensation of Z can be calculated for comparison with power theory approaches based on an ideal voltage source; but it only adjusts the impedance factor and cannot give full compensation in a practical power system.
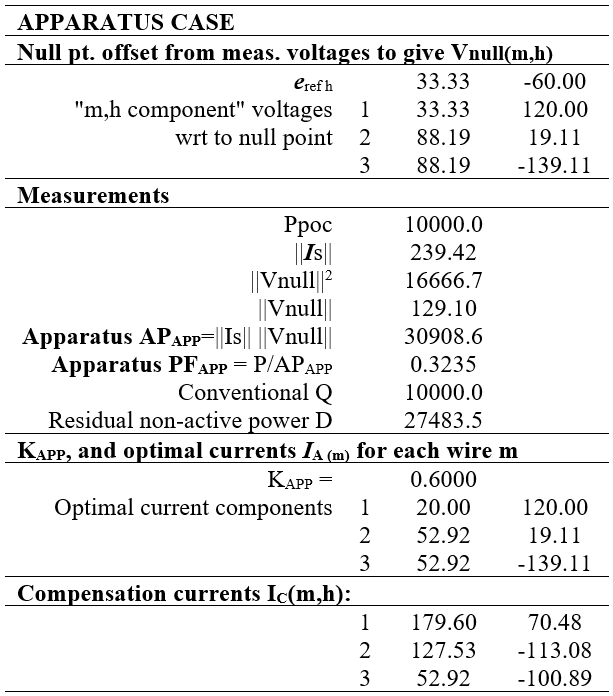
Table V - Measurement and compensation for Figure 3 Apparatus case
The GPT-adapted approach does not need the symmetrical component voltages to be calculated and has fewer, simpler steps than the CPC approach. It requires no concept of reactive power, although Q=VIsinϕ can be calculated for each h and summated. A ‘residual non-active power’ determined from PPoC, Q and APAPP of Table V corresponds to the extra CPC component
DU=27.5 kVA [25] in this unbalanced system.
3.5 Example of a simple dc system
The GPT applies to all wired power systems, so consider a 3-wire dc smart grid example (Fig. 1) with equal wire resistances delivering power to a resistive load at different voltages, as illustrated in Fig. 4. The load, an assembly of resistors, is defined only by the currents and voltages at the PoC. The question is, “what optimum wire currents would deliver the power to the load with the minimum loss?” The GPT applies to this system too.
3.5.1 Calculations
The PoC reference is the third wire. With U = {109, 47, 0}; IS = {100, 100, -200};
then PPoC = < U, IS > = 15600 W.
The weighted current vector is IS’, the product of IS and the matrix R1/2 {by (15) in [2]}, in which R(diag)= {0.01, 0.01, 0.01}, then, ||IS’||2 = <IS’, IS’>=100+100+400=600 W of line loss; giving PTh = PPoC + ||IS’||2 = 15600+600 = 16200 W.
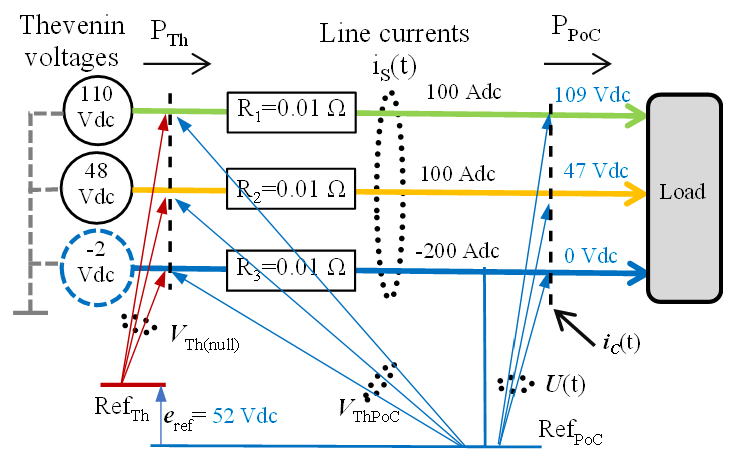
Figure 4 – DC system with three unbalanced voltages and wires of equal resistance to resistive load
The equivalent source line voltage with respect to original PoC side common reference is VThPoC = {110, 48, -2}.
The weighted null point necessary offset to subtract from above to obtain VTh_null (or VTh_null(m,h) in full) is
eref= 52 V, (by V1r1 + V2r2 + V3r3)/(r1+r2+r3)
giving VTh(null)= {58, -4, -54}.
The proportionality constant KA, is derived from the resistance-weighted voltage vector
||VTh’||2 = < VTh’, VTh’> = 582/0.01 + (-4)2/0.01 + (-54)2/0.01 = 629600,
and the minimum delivery loss {by (33) in [2]} is
||IA’||2 = ½(-||VTh’|| -/+ √((||VTh’||2 + 4 PPoC)) = 406.96 W,
identifying the optimum power sent out from the Thévenin point:
PTh = PPoC + ||IA’||2 = 16006.96 W.
This gives: KA = PTh-opt / ||VTh’||2 = 16006.96 / 629600 = 0.2542
Then the optimum wire currents IA are: KA VTh /R = {147.46, -10.17, -137.29}
The voltages at the PoC after compensation would change from U = {109, 47, 0} to U# = {109.15, 48.73, 0}, making the delivered power 15600 W, the same as before compensation.
3.5.2 Interpretation of dc system
The theory underlying this dc example is simply the algebraic calculation of currents, voltages and voltage drop, and power and losses in a power system, such that the delivery loss after compensation is the minimum possible. As Karapetoff discussed in his analogy [29], the delivery to the customer is unchanged by a redistribution of the currents to minimise the losses, but it makes a difference to the source and delivery capacity of the supplier.
In the dc power system of this example, the PFSYS can be calculated for the improvement that optimum currents distribution makes to the losses: ||IA’||2 / ||IS’||2 = 406.96 / 600, giving PFSYS = 0.82 for the dc system before (or without) compensation. By extension, APSYS=P/PFSYS = 15600/0.82 = 19024 W.
This APSYS is equal to the power (fully compensated) that could be dispatched for the same losses (600 W) as the original uncompensated power.
The example shows the GPT approach can improve the operation of multi-wire dc networks by controlling a converter for a load or source.
Traditionally, there is no apparent power or Q in dc systems, but the physics-based theory derives APSYS and PFSYS for systems with ac, dc, or mixed ac/dc components.
3.6 What about reactive power Q?
We cannot find in the GPT for systems any relationship the same as reactive power. The derivation and proof of the GPT in the frequency domain [2] showed that the delivery loss cannot be associated with Q orthogonal to P as depicted in the PQS power triangle. It was not our intention to challenge the validity of the concept of reactive power and despite all the evidence it took us a long time to appreciate that a physics-consistent concept model of power delivery cannot accommodate a physics-violating parameter like reactive power. Like every other electrical power engineer, our training and experience limited our ability to accept this obvious, apparently novel idea.
The early (mis)conception of the PQS triangle arose from a definition by Kennelly [9] deriving reactive and apparent power as Watts. With an example of a current I=4000 Arms through a single-phase RXL (series) impedance, he presented two sets of triangles in the complex plane, including those in Fig. 2. The potential difference across the resistance, pd = IR = 2000 V dissipated a power of I2R = 8 MW. The “reactive” pd = jIXL = 750 V was extended to the “reactive” power of jI2XL = 3 MW.
The power and reactive power are written in complex arithmetic with modern symbols as P+jQ=VI(cosα + jsinα). The inner product reactive power Q=<V, I> is an imaginary, axial power orthogonal to the complex plane. The arithmetic products S=VI and Q=VIsinα are measurements based on physical quantities, but they do not give physical power. They are operations applied to two complex numbers (usually defined arbitrarily as rms quantities without reference to distortion, or as measurements from a particular wire without reference to unbalance) and are not physical quantities.
The linear algebra expression is consistent with what was already well known by 1901 – that the electromechanical (physical) measurement of reactive power or energy needed a 90° phase shift and measurement of the real power or energy [30]. Realising no power is associated with reactive power, the unit of measurement was changed to volt-amp-reactive and var. Now, a digital relay can easily make a calculation neglecting the orthogonality constraint, mimicking Kennelly’s original error.
For the whole system, the loss avoided by compensation is ||IC'||2+2<IA', IC'>. Since IA' = IA x R-1/2, the product of a vector and the matrix of wire resistances, IA and IC are orthogonal only when all the wire resistance are zero. In practical systems (not assuming lossless delivery), the minimum delivery loss occurs when IA and IC are not orthogonal, which contradicts the definition of conventional Q.
The error of the power triangle arises from various factors such as disregarded zero voltage and current components, reverse harmonic power flow, unbalance, and volt drop across line impedance.
In terms of the circuit theory of electric power systems, the concept of reactive power as the oscillating component is not credible, even for an undistorted single-phase lossless system. Fig. 5 clearly shows that Q is not quantitively the same as the negative power flowing back to a source or oscillating instantaneous power within a cycle, and if it were, what would be the interpretation of other components of non-active power that have been associated with unbalance or distortion? The non-active component of current that contributes to delivery loss does not deliver non-active power; it delivers zero power.
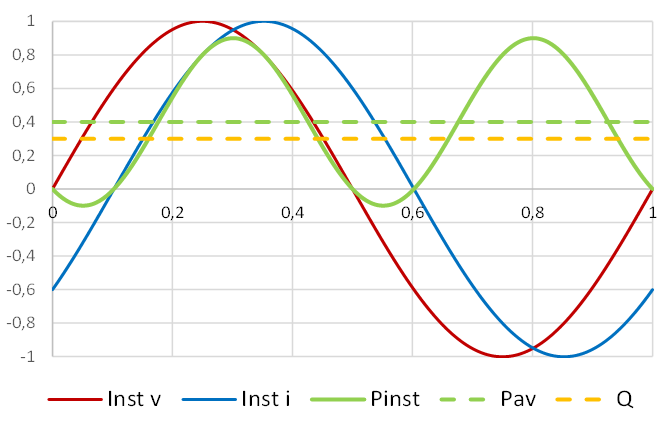
Figure 5 – Instantaneous voltage, current, power and PAV and Q during one cycle. Conventional pf=0.8
The argument that the quantities of apparent and reactive power have already proved useful, even if they are inconsistent with physics, ignores the inherent inaccuracies.
Reactive power is not a physical power, and reactive energy is not physical energy. Neither represents a quantity of losses in the delivery system. Though widely used, Q loss and kvarh in transformers and systems are not physical quantities and are algebraically zero. They, and any other defined orthogonal non-active power components, are not consistent with the law of energy conservation. Thus, common statements like “absorbing reactive power to control the voltage”, “reactive power injection” and “Q reserve margins” are inaccurate in real systems. What these terms refer to are the addition or reduction of non-active current components that do not contribute to delivering power but do incur avoidable losses in delivery. It is shown in later sections that the inaccuracies can be misleading.
Representative measurement needs a valid concept model and mathematics adequate to represent the physical relationship. Apparently without comprehending the significance of violating the laws of physics, the operational measurement of Q, a zero average quantity, has been defined as a real quantity by standards authorities, used by engineers to analyse power systems, and built into economic models and regulatory policies.
The testing of the GPT in section 4 and the practical applications of sections 5 to 9 are relevant to correcting the concepts that have been based on reactive power and energy.
4. Testing the GPT
Testing any novel analytical approach proceeds in stages. First, an example from another power theory was used in sections 3.1 to 3.4. In section 4.1, that power system is extended using another published example, one with unbalance and harmonic components. In section 4.2, the GPT in the frequency domain is compared with a different approach – time domain simulations in EMT software. Eventually, given the novelty of the implications of the GPT, it is necessary to test its validity by physical implementation in hardware, which is discussed briefly in section 4.3.
4.1 Comparison with published examples
Most published power theory examples are trivially simple with a single-phase system, an apparatus with balanced voltages or loads, or an undistorted waveform, or the examples declare insufficient data to replicate the solution. Exceptions include the examples used by Lev-Ari et al., from whom one [31] was analysed in the GPT theory paper [2], and some using the CPC approach [19], [27], [32].
Bhattarai’s thesis Illustration 5.1, with unbalance and distortion [27], depicted in Fig. 6, represents supply to an arc furnace with one phase open. The system has three wires, derived voltages from an isolated reference point that effectively adds a fourth wire, three harmonic components and no dc component. The currents and voltages at the PoC are declared as CRMS quantities and the equivalent circuit impedances are given. This is a variation of another 3-wire circuit [32] with different source impedances and only fundamental frequency components. Although the given source voltages and load impedances would not be available in a practical system, they are useful for checking the measured quantities for replicating the example.
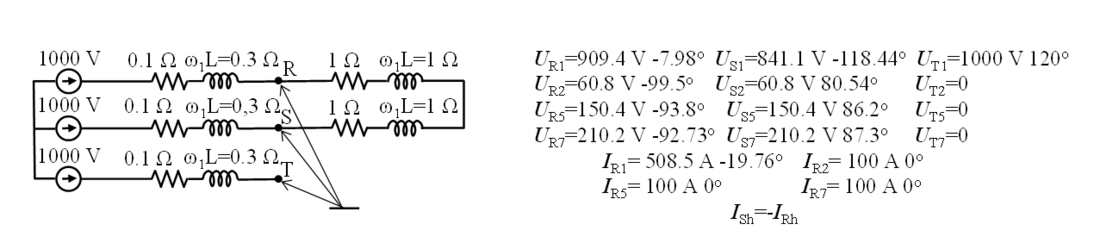
Figure 6 – Form and values of a 3-phase, 3-wire supply to an arc furnace with one phase open (arc extinguished) based on Bhattarai’s Illust. 5.1 of [25]. The artificial voltage measurement reference, which is not a system wire, adds a 4th wire, and voltages and currents are provided as CRMS amplitude and angle
Compared with Fig. 3, this example adds a fourth wire, even though it is only a reference point for measuring voltages. The wire carries no current, so it is connected to the Thévenin point by a high impedance. The three harmonic components require superposed circuits with the same topology as the fundamental frequency, illustrated in Fig. 7 for only the fundamental component h1 and one distorting harmonic h5, each requiring the same calculation routines, and with results collected for the whole system.
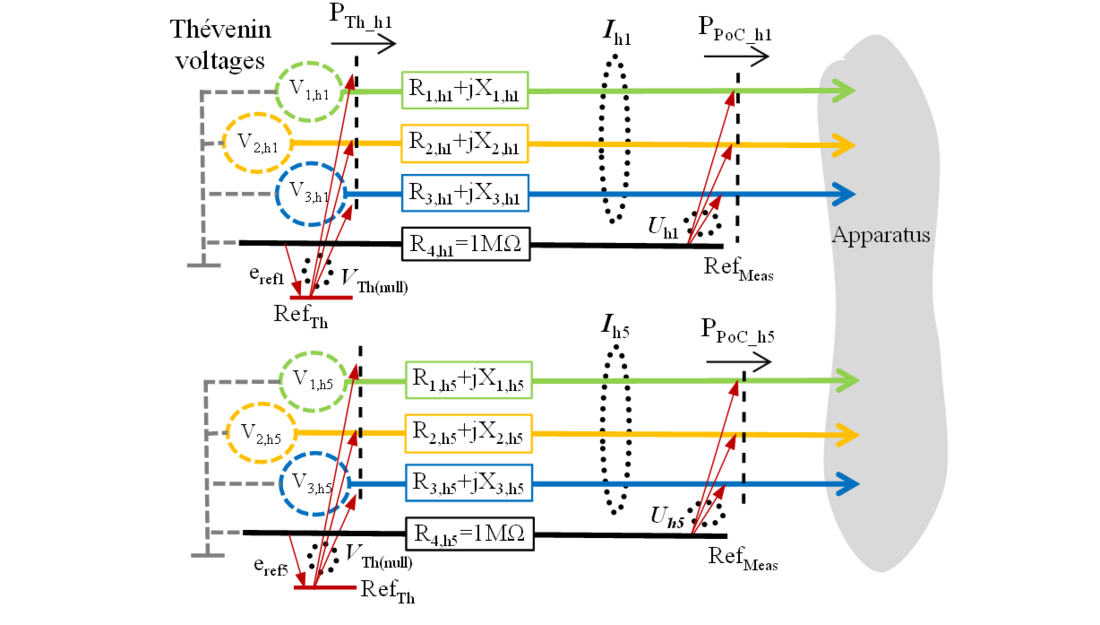
Figure 7 – Concept model of power system represented by the Thevenin equivalent circuit ‘lines’ for a 4-wire system with two phases, a neutral and a virtual voltage measurement reference point – and a fundamental and 5th harmonic
Key results of the GPT and CPC analysis are presented in Table VI.
For an apparatus connected at the terminals R, S and T, the CPC quantities for power, PFAPP and APAPP [27] are the same as those of the GPT apparatus case, confirming the validity of CPC analysis for this topology. However, the apparatus is supplied by a power system that is neglected in calculating these quantities.
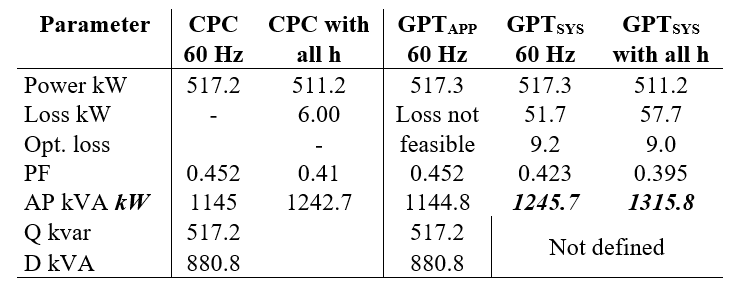
Table VI - GPT quantities for an unbalanced load in the power system of Fig 6 compared with CPC analysis [25]
Bhattarai’s analysis indicated a loss of 6 kW in the power system – the difference between the fundamental power of the apparatus and its power with all frequency components. The GPT analysis shows instead that some power (6 kW) is returned to the power system by the harmonic components. A meter that measures only filtered fundamental frequency components would ‘over-read’ by 6 kW the net power delivered to the load, but that 6 kW represents real power re-transmitted into and dissipated in the delivery system.
The delivery of total (net) power at the PoC of 511.2 kW at all frequencies incurs a system loss of 57.7 kW. The loss could be reduced to 9.0 kW by effective compensation, and without compensation is reflected in the low PFSYS=0.395 for the load at the PoC.
Without compensation, the injection of harmonic power into the system is a consequence of the waveform distortion by the nonlinear load. A ‘source’ of power at a harmonic frequency is possible even when a customer’s load has no embedded generation. To draw power most efficiently from the supply system, a GPT-controlled compensator will not inject harmonic power to the system, since to do so would incur losses without contributing to the power required at the PoC. Also, it would not draw at the fundamental frequency the re-exported power.
4.2 Comparison with time domain simulation
The results of GPT analysis have been compared with simulations in PSCAD/EMTDC and MATLAB/Simulink. Both these time-step simulation tools can represent the power system response at any frequencies. They differ from conventional load flow software based on fundamental-frequency power system equations with intrinsic reactive power concepts. Both simulation packages allow the system to be defined as a network with resistance and inductance, and with voltage sources. Loads can be represented by the PoC currents or impedances without having to define power and reactive power. And both give the same results in simple simulations.
In making comparisons between the GPT analysis and time domain simulations, the equivalent or ideal voltage sources at the Thévenin point and the PoC currents are input from the GPT spreadsheet without compensation and then with the compensation suggested by the GPT spreadsheet. Testing progressed through stages of balanced systems with only fundamental frequency to more complex unbalanced distorted conditions. The apparatus case can be approximated by setting the equivalent circuit impedances close to zero without the software defaulting to zero.
The circuit of the fundamental frequency subsystem of Fig. 7 for MATLAB Simulink simulation is illustrated in Fig. 8. The reference point for the measurement of PoC voltages is constructed by a high impedance separation from the neutral of the Thévenin sources.

Figure 8 – Circuit for testing in MATLAB Simulink the system of Fig 6. Only the subsystem of one of the four frequency components (fundamental and three harmonics) is depicted
In all cases tested, before and after compensation, the simulations return the same losses and PoC voltages as predicted by the GPT spreadsheet. This confirms the frequency domain calculations of the GPT are consistent with time domain simulation. The minimum loss combination of current components is available only with the mathematical proof in the GPT derivation [2], so simulations could verify the GPT’s optimisation only by infinite testing. However, the time domain simulations can show that other compensation approaches do not achieve the optimum loss reduction of the GPT approach.
Testing against other methods of calculating compensation requires that full numerical details of those other methods are available for making comparisons. At this stage, few such examples have been identified. The constraint is not on the size of the example, since the GPT is independent of network size. The GPT ‘sees’ the network only from the PoC, and the equivalent circuit impedances of any network are derived from measurement or conventional simulation. The main constraint is that few optimum loss solutions of test cases with unbalance and distortion have been published, and we have tested most of those available. Another constraint is that few test systems with unbalance and distortion have been endorsed by the engineering community. Therefore, for the analysis of the GPT applications in the following sections, we have adapted existing test systems or derived new ones appropriate to the problem being investigated.
4.3 Physical system testing
Since the GPT is developed on a physics-based concept model of a power system, it should be possible to test its validity by measurement on a physical power system. Physical testing of GPT-controlled inverters has already begun [33]. Testing of the GPT concept involves Control- and Power-Hardware-in-the-Loop (referred to as CHIL and PHIL tests) and Real-Lab tests in a microgrid that can be controlled, modelled, and represented completely by only the voltages, currents, power and equivalent circuit impedances at the PoC.
APPLICATIONS
The GPT is not merely a new computer game; its concept model is practical and useful because it is consistent with the laws of physics and the behaviour of the power system. The sections 5 to 9 describe the link between engineering science and engineering practice through theory-based applications.
5. GPT control of distributed generation
Distributed generation (DG) is implemented widely on distribution systems in developing and developed countries. The typical mix of large and small, three- and single-phase customers, and variable loads results in constantly changing unbalance during different times and seasons. DG is widely considered to reduce feeder losses, but voltage rise with increasing DG penetration is a constraint requiring control. In this section, the implications of the GPT for controlling power injected from a distributed energy source into an unbalanced feeder without distortion are examined.
The system performance can be demonstrated in a medium voltage feeder with distributed loads and a DG source, and the same principles apply to the connection of large generators and transmission networks to distribution utilities.
It is useful first to consider:
- the nature of the currents drawn from the original (main grid, bulk) source when energy is injected elsewhere in the feeder; and
- the loss attributable in the GPT to a load at the PoC when there are other loads on the system.
5.1 Effect of power input to downstream network
As energy is injected by DG into a feeder (or minigid or any secondary network) with distributed loads, the power drawn from the main source reduces. Usually, power from converter based “renewable” DG sources is injected at conventional unity power factor, with equal currents in phase with the terminal voltages. The feeder’s bulk source supplies the balance of the currents not supplied by the DG.
5.2 Loss reduction in multi-node systems
Consider two separate resistance loads I1 and I2 at a PCC at the end of a very simple feeder of resistance r. Since they share the delivery system resistance r, the total loss dissipated by the two currents is (I1+I2)2r = (I12+I22+2I1I2)r. According to the GPT, the loss attributable to I1 is I12r1Th and to I2 is I22r2Th. However, neither load is observable by the other except by its effect on the Thévenin equivalent impedance seen from each load’s PoC, so the term 2I1I2r of loss cannot be calculated for an individual PoC. If both currents supply loads, the terms I12r and I22r will under-estimate the feeder loss. If one current is a source (such as from a DG) reducing the load current in any branch of the feeder, the actual loss will be over-estimated by the individual terms.
This effect is like the GPT’s loss reduction by compensating the non-active current components, with the avoided loss given by ||IC'||2+2 <IA', IC'>. Unlike the GPT’s capacity to calculate the current distribution to eliminate IC, the currents at other PoCs on the system are not observable to a meter or compensator at its PoC. Therefore, estimates of total loss before compensation ||IS'||2 and after compensation ||IA'||2 differ from the actual loss incurred in the system by combination with other PoC currents.
Nevertheless, reduction of one current term at a PoC will reduce the loss attributable to all PoCs. Complete loss optimization is possible only by reducing the avoidable loss at all nodes.
In this section, GPT-based control will be considered only for the DG source and at the input to the feeder from the main source.
5.3 Distributed generation control
Most renewable energy sources and other novel technologies like battery storage and EVs, require power electronic converter interfaced technologies with suitably controlled power/energy injection. In some cases, the integration of renewable energy has led to problems, including voltage control, that have been measured in real systems [34].
Most DG is located near the electrical edges of power systems where voltages, inertia and fault levels are relatively low, and distortion and unbalance are significant. Most distribution systems were originally designed to meet the voltage drop constraints of passive feeders supplied from central generation. In some feeders, shunt capacitor banks are installed to support the voltages; an approach referred to as volt-var control (VVC).
DG can reverse the direction of power flow in all or part of an existing passive feeder, changing the voltage profile, and even causing voltages on the feeder to exceed the usual limits. In the same way as VVC using capacitors supports voltages on a passive feeder, VVC can also ‘absorb inductive reactive power’ at a DG node to reduce the voltage rise, allowing more power and energy to be injected into the feeder [35] [36] [37].
5.4 DG on a medium voltage feeder
The following simplified example investigates the optimum control of DG on an unbalanced medium voltage (MV) feeder. The effects of VVC to limit voltage rise at the DG terminals are compared with GPT-based control. Instead of the approximations of reactive power and conventional power factor, the GPT offers an approach consistent with the physics of power delivery.
5.4.1 Feeder model
Despite the availability of MV test feeders [38], [39], a simpler example is sufficient to demonstrate the effects of the DG and the application of GPT analysis. An originally passive rural distribution feeder, extended to a DG at Bus 6, shown in Fig. 9, represents typical development of new renewables-based DG.
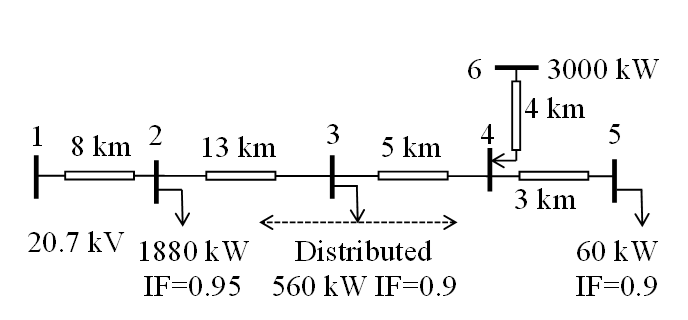
Figure 9 – Converter-based DG at Bus 6 exporting power into a 20 kV rural feeder with unbalanced line parameters and unbalanced loads. IF=R/Z
The maximum output of the new DG could exceed the feeder demand during periods of high generation. This example considers only DG output below the level of causing reverse power into the source network.
The three-phase delta feeder is rated 20 kV (line to line). It operates at 50 Hz and is without distortion. The ideal voltage source at Bus 1 represents a strong supply to a town, with the rural feeder supplied from a busbar controlled at 20.7 kV. The line conductor is ACSR Fox. Line impedances and shunt susceptance are slightly unbalanced as shown in Table VII.
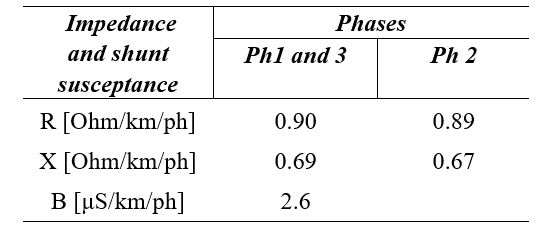
Table VII - Line impedances at 50 Hz
Intermediate loads shown in Table VIII introduce unbalanced currents and voltage drop along the feeder, without causing distortion. The loads draw constant power with constant impedance factor R/Z equal to conventional pf. Loads without voltage control on LV and MV feeders typically have a mixed character and can be modelled as constant currents.

Table VIII - Loads on the 20 kV rural feeder
The purpose of this example is not a worst-case design or identification of limits of penetration, so the loads are modelled as power to establish a constant value of power delivered. This approach simplifies interpretation of the trends of other parameters, and extrapolation of the performance to high voltage systems.
The Thévenin equivalent impedance of the shunt-series feeder impedances, as seen from a PoC, can be extracted using a Simulink measurement impedance block suitable for 3-wire systems.
Conventional inverter control injects equal currents into each phase, aligned with the voltage. The injected power raises voltage levels in the vicinity of the DG bus and may cause voltages to rise above an acceptable level, assumed in this example to be a commonly applied limit of 1.075 p.u. (7.5% above rated voltage).
The feeder is modelled in MATLAB/Simulink by defining loads as impedances to avoid any uncertainty associated with the concept of Q, and adjusting those impedance magnitudes to maintain constant load power. The optimum compensation by the DG inverter is calculated according to the GPT using the same processes in MATLAB as in the Excel spreadsheet. As explained in section 5.2, the loss uniquely attributed to the DG input by the GPT does not account for the combined load and DG loss in the feeder, so the total feeder loss must be calculated in the MATLAB simulation.
5.4.2 Feeder voltage profile
The voltage profiles along the passive feeder and for an active feeder with balanced DG input per phase are depicted in Fig. 10. The maximum phase voltage at Bus 6 reaches the upper acceptable limit of 21.5 kV when the DG output reaches about 1800 kW at conventional pf=1. At DG output of 2736 kW the limit of this model’s assumptions is reached with reverse power into the source bus.
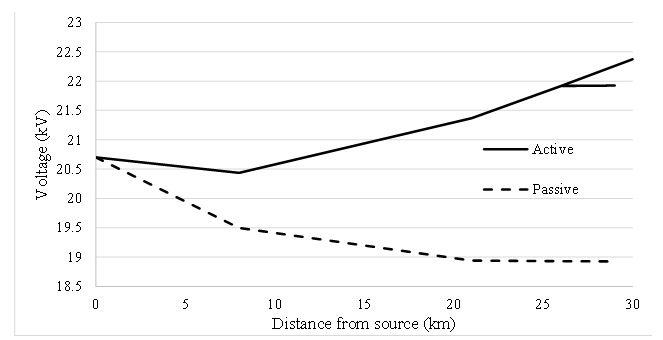
Figure 10 – Voltage profile of feeder. Passive feeder, DG=0, dashed. Active feeder with DG=2.7 MW at conventional upf shown solid
5.4.3 Losses
As the DG input to the feeder load increases, the feeder losses decline until the demand is met with about 1000 kW from the DG and the balance from Bus 1. Higher DG export increases the feeder loss. The feeder loss is depicted by the black dashed line in Fig. 11.
Instead of conventional DG control, the inverter can be controlled according to the GPT, injecting current into the wires inversely to their Thévenin equivalent resistance. On its own, the GPT control of the DG reduces the losses very little, as depicted by the dashed blue line, since the feeder draws current from the strong source at Bus 1, even when the DG supplies all the power of the feeder loads and loss.
When the DG power level increases voltages above the limit, the feeder’s DG capacity is increased by VVC. The typical inverter’s absorption of “reactive power” at the DG terminals is achieved in this example by adding controlled shunt inductances. The different (less optimal) set of currents includes reactive current components that incur avoidable loss without delivering power. The loss curve with VVC is depicted in maroon in Fig. 11. The VVC enables more power to be injected by the DG, but one third of the extra DG export enabled by the VVC is dissipated as losses.
Simultaneous GPT control and VVC by reactors demonstrates the two approaches are incompatible because the GPT-controlled inverter currents offset the avoidable loss introduced by the VVC and restore the voltage associated with efficient delivery.
The VVC use of “reactive power” (more accurately non-active current components) for voltage control is apparently widely used. In this example, it increases revenue for the power producer, but the high avoidable losses reduce the benefits for the distribution system operator and the customers.
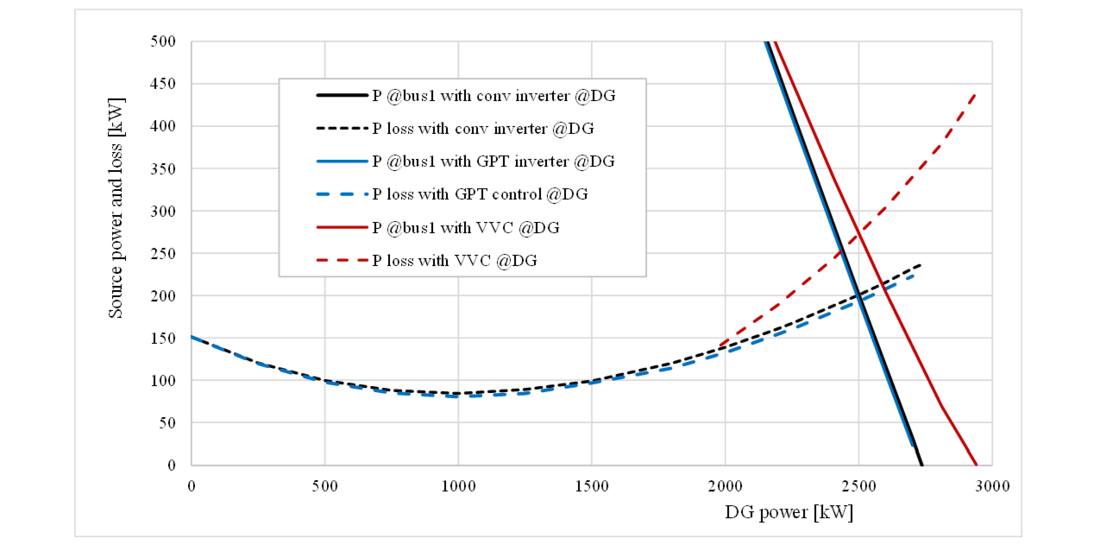
Figure 11 – Grid source power (solid) and feeder loss (dashes) in response to increasing DG power injection. GPT inverter control (blue) has small effect. VVC (maroon) suppresses voltage rise above 21.5 kV, but extra losses reduce effective DG power
5.4.4 Currents from the strong source
Since the DG input to the feeder can be controlled to provide only power, as the DG contribution increases, an unconstrained feeder will draw from the bulk source a higher proportion of currents not contributing power.
A GPT-meter at Bus 2 on the incoming line from Bus 1 can measure the power, apparent power APSYS, and PFSYS of the currents drawn from the source. The contribution from the strong source is depicted in Fig. 12.
As PDG increases, the power supplied from Bus 1 decreases until the voltage at Bus 6 reaches the limit value. APSYS remains high relative to the real power supplied and the PFSYS decreases steadily.
If the DG power level is increased and the maximum voltage on the feeder is limited by VVC, the DG power can be increased until negligible power is drawn from Bus 1. The dashed extensions to the curves in Fig. 12 show how the GPT-based PFSYS measured at the Bus 2 Incomer reduces to nearly zero and the maximum power that could be sent out from the source for the same loss (APSYS) increases rapidly when VVC is implemented.
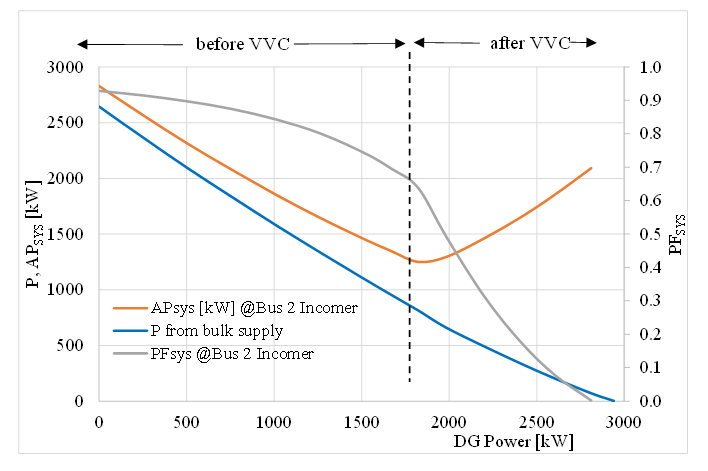
Figure 12 – GPT metered feeder load received at Bus 2 from Bus 1
These results cannot be compared with those of conventional meters because the current components imported by the feeder from the bulk supply are unbalanced, and conventional 3-phase apparent power and power factor equations are not defined for unbalance. Even reactive power meters complying with the same standard specification give different measurements according to their proprietary design [15].
GPT-controlled compensators can eliminate the current components that deliver no power but incur delivery loss. GPT-controlled compensation at the incoming supply to Bus 2 from Bus 1 and at the DG bus significantly reduces the feeder loss, as illustrated in Fig. 13. There is no demand for ancillary service from the bulk source, and the voltage limit is not exceeded for DG power up to 1800 kW. However, achieving this condition requires that the export of power from the DG into the feeder be limited, not increased by causing extra loss.
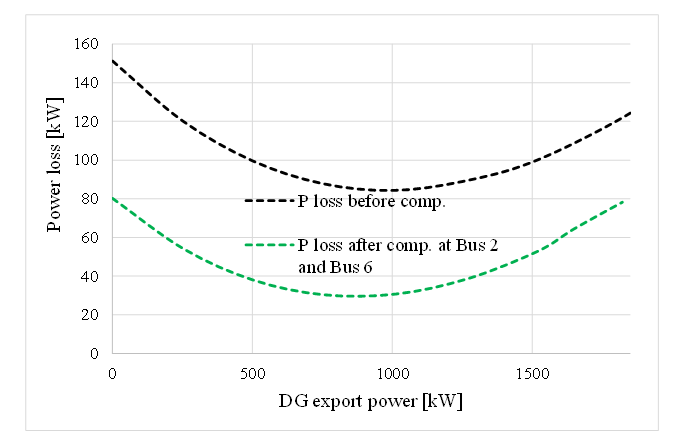
Figure 13 – Loss reduction with a GPT-controlled inverter on the DG at Bus 6 and by a GPT-controlled compensator at the Bus 2 Incomer from Bus 1
5.4.5 Interpretation of the feeder performance
A simple distribution feeder exposes the weaknesses of conventional reactive power thinking about controlling feeders. VVC by reactive power absorption to limit voltage rise on a feeder and enable higher outputs from DGs is possible but incurs high losses.
MATLAB simulations and GPT analysis together show that:
- GPT-control of an inverter for loss minimisation is incompatible with “reactive” VVC that enables higher DG export by incurring significant losses to reduce the voltages at the DG terminals.
- The existing control of DG puts extra demand on bulk suppliers for ‘ancillary services’ and reduces the suppliers’ relative efficiency of delivery – evidenced by PFSYS and APSYS. Traditional power theory and standards-compliant meters cannot reliably identify these effects.
- GPT compensation at the feeder connection to the bulk supply can eliminate the nonactive ‘power’ drawn from the bulk supply and improve the feeder performance.
There are implications for system planning, the approach to optimal power flow, metering, and the financial compensation of suppliers that meet the power balancing needs of distributors and customers with generating capacity “behind the meter”. The value of DG energy after losses, and cost reflective charging for the balance of currents drawn from the bulk supply are commercial issues that need to be informed by the technical behaviour of the power system.
The lessons from the analysis of this MV feeder extend also to lower and higher voltage systems. At high voltage, the bulk supplier might be a transmission operator, and the feeder represent the network of a distribution utility. Traditional power theories, which cannot represent practical system performance, confuse the decision-making about the ancillary services from bulk suppliers. As more converter interfaced generation connects at distribution levels and displaces energy supplied from transmission networks, new technical and commercial arrangements will be required [40].
This example is limited. It has not analysed feeder performance with mixed power and impedance load models or the effects of harmonic distortion. A feeder with lower load and high DG injection, such as at night with wind generation, could reverse power flow into the voltage source bus and violate the model assumptions. Analysing a feeder with reverse power would need a different source model, and voltage control at Bus 1, such as by an automatic tap-changer.
Intermediate conclusions
Using several examples, the GPT-based model-and-process measurement of power parameters at a PoC has been compared with other approaches to power, reactive power, and apparent power. Our research shows that the understanding of power parameters at an apparatus is complemented by considering the whole system from sources to loads. The GPT approach, with a concept model compatible with the laws of physics and accommodating unbalance, harmonics, and the delivery system, avoids the traditional approaches’ assumptions that are violated in practical power systems.
An infinite combination of current components in the Hilbert space of voltage and current vectors can deliver power to a PoC, but only one combination will do so with the minimum loss. Linear algebra offers a rigorous and compact way of representing the relationships between all the variables and identifying the unique, minimum-loss combination and the ‘real’ power dispatched, dissipated as delivery loss, and delivered. The GPT measurement can be extended to identify how a load or distributed source can be compensated to achieve the optimum of minimum loss.
The GPT cannot accommodate reactive power Q that is defined as an arithmetic product of a voltage and an orthogonal current component, and which, when voltage and current are treated as vectors in linear algebra, is always zero. Similarly, historically defined apparent power is also an operational measurement with no direct physical meaning, but its form can be defined in the GPT as a physical power measured in Watts, conditional on the voltage-current displacement being corrected.
Tested using EMT simulation, the GPT approach compares favourably with conventional Q-based power theories. As an example, conventional power theory suggests volt-var control of DG, whereas the GPT exposes its disadvantages in terms of losses. Part 2 of this paper examines further examples and implications of the GPT.
Acknowledgements
George Gabriels provided the Thévenin impedance measurement meter in MATLAB/Simulink for measuring equivalent circuit parameters from a PoC.
The research has been funded in part by a grant from the Open Philanthropy Project.
References
- C.P. Steinmetz, “Symbolic representation of general alternating waves and of double frequency vector products,” Trans AIEE, vol. XVI, pp. 269-296, 1899, doi: 10.1109/T-AIEE.1899.4764075.
- M. Malengret and C. T. Gaunt, “Active currents, power factor, and apparent power for practical power delivery systems”, IEEE Access, 2020 doi: 10.1109/ACCESS.2020.3010638.
- M. Malengret and C. T. Gaunt, “Decomposition of currents in three- and four-wire systems,” IEEE Trans. Instr. and Measurement, vol 57, Issue 5, pp 963-972, 2008, doi: 10.1109/TIM.2007.911705.
- M. Malengret and C. T. Gaunt, “General theory of instantaneous power for multi-phase systems with distortion, unbalance and direct current components,” Electr. Power Syst. Res., vol. 81, pp 1897-1904, 2011, doi: 10.1016/j.epsr.2011.05.016.
- M. Malengret and C. T. Gaunt, “General theory of average power for multi-phase systems with distortion, unbalance and direct current components,” Electr. Power Syst. Res., vol. 84, pp. 224-230, 2012, doi: 10.1016/j.epsr.2011.11.020.
- C. T. Gaunt and M. Malengret, “True power factor metering for m-wire power systems with distortion, unbalance and direct current components,” Electr. Power Syst. Res., vol 95, pp. 140-147, 2013, doi: 10.1016/j.epsr.2012.07.019,
- M. G. Simões, F. Harirchi, and M. Babakmehr, “Survey on time-domain power theories and their applications for renewable energy integration in smart-grids”, IET Smart Grid, vol. 2, issue 4, p.491–503, 2019, Doi: 10.1049/iet-stg.2018.0244
- A. E. Kennelly, “Impedance”, Trans. AIEE, vol X, p175-232, 1893. doi: 10.1109/T-AIEE.1893.4768008.
- A. E, Kennelly, “Vector power in alternating-current circuits”, Proc. AIEE, vol. 29, issue 7, p1023-1057, 1910. doi: 10.1109/PAIEE.1910.6659879.
- F. B. Silsbee, “Power factor in polyphase systems”, Trans. AIEE, vol. 39, issue 2, p1465-1467, 1920. doi: 10.1109/T-AIEE.1920.4765336.
- J. A. Suul and M. Molinas, “Properties of reactive current injection by AC power electronic systems for loss minimization”, 15th Int. Power Electronics and Motion Control Conf. (EPE/PEMC), Serbia, 2012. doi: 10.1109/EPEPEMC.2012.6397415.
- Electropedia, IEC Electrotechnical Vocabulary, available online at http://dom2.iec.ch/iev.
- DIN 40110 Quantities used in alternating current theory; Part 1 (1994): Two-line circuits; Part 2 (2002): Multi-line circuits.
- IEEE Standard definitions for the measurement of electric power quantities under sinusoidal, nonsinusoidal, balanced, or unbalanced conditions, IEEE Standard 1459-2010.
- NEMA C12.24 TR-2011 “Definitions for calculations of VA, VAh, VAR, and VARh for poly-phase electricity meters” 2011, National Electrical Manufacturers Association, Rosslyn, USA.
- A. J. Berrisford, “Smart meters should be smarter”, IEEE Power and Energy Society General Meeting, San Diego, USA, 2012. doi: 10.1109/PESGM.2012.6345146.
- C. Ndungu, private communications, Sep 2020 – Nov 2021.
- L. S. Czarnecki and P. D. Bhattarai, “Reactive compensation of LTI loads in three-wire systems at asymmetrical voltage,” Int. School on Nonsinusoidal Currents and Compensation (ISNCC), Lagow, Poland, 2015 doi: 10.1109/ISNCC.2015.7174712
- L. S. Czarnecki and P. M. Haley, “Unbalanced power in four-wire systems and its reactive compensation,” IEEE Trans. Power Del., vol. 30, no. 1, pp. 53-63, 2015, doi: 10.1109/TPWRD.2014.2314599.
- L. F. Correa Monteiro, B. F. Exposto, J. G. Pinto, M. Aredes, and J. L. Afonso, “Control algorithms based on the active and non-active currents for a UPQC without series transformers,” IET Power Electron., vol. 9, no. 9, pp. 1985_1994, 2016, doi: 10.1049/iet-pel.2015.0642.
- C. Burgos-Mellado, R. Cardenas, D. Saez, A. Costabeber, and M. Sumner, “A control algorithm based on the conservative power theory for cooperative sharing of imbalances in four-wire systems,” IEEE Trans. Power Electron., vol. 34, no. 6, pp. 5325_5339, 2019, doi: 10.1109/TPEL.2018.2869866.
- H. K. Morales Paredes, F. P. Marafao and L. C. P. da Silva, "A comparative analysis of FBD, PQ and CPT current decompositions — Part I: Three-phase, three-wire systems," IEEE PowerTech, Bucharest, Romania, 2009, pp. 1-8, doi: 10.1109/PTC.2009.5282173.
- H. K. Morales Paredes, F. P. Marafao and L. C. P. da Silva, "A comparative analysis of FBD, PQ and CPT current decompositions — Part II: Three-phase four-wire systems," IEEE PowerTech, Bucharest, Romania, 2009, pp. 1-6, doi: 10.1109/PTC.2009.5282169.
- H. Lev-Ari, R. D. Hernández, A. M. Stanković, and E. A. Marengo, “Adaptive near-optimal compensation in lossy polyphase power systems,” IEEE Trans. Control Syst. Techn., vol. 26, no. 2, pp. 732-739, 2018, doi: 10.1109/TCST.2017.2677742.
- L. S. Czarnecki and P. D. Bhattarai, “Currents’ physical components (CPC) in three-phase systems with asymmetrical voltage,” Przegląd Elektrotechniczny, R. 91, Nr. 6/2015, doi: 10.15199/48.2015.06.06.
- D. I. Brandao and E. Tedeschi, “Three-dimensional representation of electrical circuit quantities,” IEEE Trans. Power Syst., vol. 35, no. 4, pp. 3258-3261, 2020, doi: 10.1109/TPWRS.2020.2967222.
- P. D. Bhattarai, “Powers and compensation in three-phase systems with nonsinusoidal and asymmetrical voltages and currents.” PhD dissertation, Louisiana State University, 2016. https://digitalcommons.lsu.edu/gradschool_dissertations/1712.
- M. Malengret and C. T. Gaunt, “Inverters and compensators for minimum line losses,” Conf. on Power Electron. and Appl. and Exhibition (EPE), Karlsruhe, Germany, 2016, doi:10.1109/EPE.2016.7695634.
- V. Karapetoff, “Contribution to discussion,” in C. Fortescue, Measurement of power in polyphase circuits, Trans. AIEE, vol. XLII, pp. 358-375, 1923, doi: 10.1109/T-AIEE.1923.5060878.
- W.H. Browne, “Power factor indicators,” Trans. AIEE, vol. XVIII, pp.287-312, 1901, doi: 10.1109/T-AIEE.1901.4764183.
- H. Lev-Ari and A. M. Stanković, “Fundamental performance limits in lossy polyphase systems: Apparent power and optimal compensation,” IEEE Int. Symp. Circuits Syst., New Orleans, LA, USA, pp. 61–64, 2007, doi: 10.1109/ISCAS.2007.378182.
- L. S. Czarnecki and P. D. Bhattarai, “A method of calculating LC parameters of balancing compensators for ac arc furnaces,” IEEE Trans. Power Del., Vol 32, Issue 2, 2017, doi: 10.1109/TPWRD.2016.2536681
- P. Jankee, M. Malengret, D. Oyedokun, and C. T. Gaunt, “An inverter controlled by the General Power Theory for power quality improvement,” 30th Southern African Universities Power Engineering Conference (SAUPEC), 2022, doi: 10.1109/SAUPEC55179.2022.9730729.
- E. Batzelis, Z. H. Rather, J. Barton, B. R. Naidu, B. Wu, et al. “Solar integration in the UK and India: Technical barriers and future directions,” JUICE White Paper on solar integration, 2021. doi: 10.17028/rd.lboro.14453133
- V.A. Evangelopoulos, P.S. Georgilakis, and N.D. Hatziargyriou, “Optimal operation of smart distribution networks: A review of models, methods and future research,” Electr. Power Syst. Res., 140 (2016) 95–106, doi: 10.1016/j.epsr.2016.06.035.
- I. Abdelmotteleb, T. Gómez, and J. P. Chaves-Avila, “Benefits of PV inverter volt-var control on distribution network operation,” IEEE PowerTech, 2017, doi: 10.1109/PTC.2017.7981098.
- A. M. Howlader, S. Sadoyama, L. R. Roose, and S. Sepasi, “Distributed voltage regulation using volt-var controls of a smart PV inverter in a smart grid: An experimental study”, Renewable Energy, 127, pp.145-157, 2018, doi: 10.1016/j.renene.2018.04.058.
- TF C6.04, “Benchmark systems for network integration of renewable and distributed energy resources,” Technical Brochure TB 575, CIGRE, Paris, 2014.
- W. H. Kersting, “Radial distribution test feeders,” IEEE Trans. Power Syst., vol. 6, no. 3, pp. 975–985, Aug. 1991, doi: 10.1109/59.119237.
- C. T. Gaunt, “Comments in response to notice of inquiry: Reactive power capability compensation,” in Federal Energy Regulatory Commission, Docket No. RM-22-2, 17 Feb. 2022.
