C3 - Impact of Climate and Weather Variability on Energy Systems Planning
Authors
Sebastian PORRAS APARICIO, Alexandre OUDALOV - Hitachi Energy, Switzerland
Georgios MAVROMATIDIS - ETH Zürich, Switzerland

Summary
Climate change is a phenomenon that has been developing during the last decades and in recent time has been identified as a major concern introducing challenges for processes like energy planning. Various locations around the world have been experiencing new environmental conditions and an increased frequency and intensity of extreme weather events. As a result, the power grid is stressed both from the demand- and supply-side, foreseeing an increase in the electricity demand and a reduction or affectation in the generation availability and efficiency. Capacity expansion planning is used for the decision-making process regarding the investment planning of an electric grid interconnection system. A key limitation of most of the current capacity expansion models lies in the fact that they consider fixed renewable (solar, wind, hydro) profiles for each year in the model horizon. Furthermore, demand profiles are produced by demographic projections without taking into consideration disturbances or modifications that the variations in some climate parameters could generate.
This paper aims to address the gap in incorporating climate variability in long-term energy planning. It proposes an approach to integrate the impact of climate and weather variations in a capacity expansion planning model and studies their impact on the European energy system planning. A model with selected European countries covering a wide latitudinal range is used to test and study the proposed approach.
The most relevant climate parameters for this study are identified. These are: air temperature, wind speed and solar irradiance, which affect the entire energy system in different areas. Then, long-term projections for each climate variable are obtained from global climate models. These projections are, first, geographically filtered and processed to obtain the representative hourly profiles for each network zone in the model, and second, used to determine the climate’s impact on the electricity demand and supply side by enhancing a capacity expansion modeling framework.
Keywords
Capacity expansion planning, climate impact, energy planning, European energy system, weather variability1. Introduction
Climate change is an ongoing phenomenon that has been taking place in Earth during the past decades, but only until recent years it has been considered as of major concern by different stakeholders of global politics and economics. The changes presented by climate change are not noticeable in small time scales, but some of these consequences are starting to become evident. Ecosystems around the world are facing environmental conditions that they have never experienced before e.g., some regions are undergoing sustained periods of temperatures above or below the normal average range [ 1], which are accompanied by record breaking peak or low temperatures during summer and winter, respectively. At the same time, the frequency and intensity of Extreme Weather Events (EWE) has been increasing at a higher rate in the last few years compared to historical trends, demonstrating tangible evidence of the climate change.
Both long-term variations of different climate parameters and the occurrence of extreme weather events have several consequences on different levels of the society, two examples are change in population behavior and impact on physical infrastructure as the power system [2]. On the first one, human beings will always seek comfort, using different technological devices for it. When it comes to thermal comfort, HVAC (Heating, Ventilation and Air Conditioning) systems are used to control the indoor air temperature and set it within the range of human comfort zone, which ranges between 22°C and 27°C. Therefore, periods with increased or decreased air temperatures lead to an increase in energy consumption due to the higher utilization of heating and cooling devices [3, 4]. On the other hand, power generation units and transmission systems are technological equipment that have an optimal operational range defined by a specific range of parameters, including weather conditions e.g., air temperature, wind speed, relative humidity, etc. If some of these parameters excurse outside the range, then the power output or transmission capacity can be affected [5, 6].
Capacity expansion modeling is used for the decision-making process of long-term investment planning of an electricity interconnected system. It takes as input several parameters from both the demand- and supply-side of the energy system and runs an energy adequacy and infrastructure planning assessment along a multi-year or multi-decade horizon. From the demand-side, the main parameters to be considered as an input are the projected demand profiles for the future investment steps, which are normally produced following specific assumptions or defined scenarios. On the supply-side, resource potentials and techno-economic data for the considered technologies and energy carriers are the common inputs to be required.
The more conventional formulation of the capacity expansion models presents some limitations both from the input data side and the problem formulation. Regarding the demand profiles used as input, they are generally based on demographic projections and energy efficiency assumptions, which may provide a good estimation, but do not consider directly possible climate and weather variability. As it was mentioned earlier, prolonged periods of increased or decreased temperatures can lead to an increase in the electricity demand, probably deviating from the demand that is estimated only using demographics. Moreover, the models would normally consider fixed renewable profiles (solar, wind, hydro) for all the future investment steps [7]. By doing so, they do not consider the natural inter-year variability of these resources, which may vary depending on the conditions of the atmospheric circulation [8], that can also be affected by the climate change. If capacity expansion planning is carried out without taking into account the impacts that the variability of climate and weather parameters can have on the system, it could lead to a scenario of energy inadequacy [5]. The main consequence of this would be the inability of the system to balance the electricity demand, resulting in unserved load that would need to be disconnected, causing repercussions beyond the technical components, incurring in high economic and social costs.
Some studies have focused on the impact of climate change on the power infrastructure and the process of long-term planning. Different response patterns of the electricity demand have been identified as a function of the air temperature [9, 10]. At a sector level, the impact of air temperature on the energy demand has also been researched for the buildings [11, 12, 13] and transport sector [14], which are determined to be the most sensible ones. The buildings sector demand is heavily influenced by the space heating and cooling, and in a future with a fully electrified road fleet, the impact of temperature in the range of electric vehicles will also influence the final energy demand of the sector.
The impact of different weather parameters on the physical infrastructure of the power system has also been studied. It is known that the ampacity of the Overhead Transmission Lines (OHL) is influenced by several of these parameters [6, 15]. On the supply-side, different generation units are affected in several ways; wind and solar generation are affected by the wind speed and the solar radiation [16]. Hydro power is also affected by the precipitation variation [17]. Moreover, conventional generation units may also be affected by the variation of the air temperature due to cooling restrictions [18].
Going beyond the only-demand or only-generation analysis, the energy adequacy assessment considering the climate change impact has also been studied [7, 19, 20]. The main challenge to overcome is the size of the problem, which is normally addressed by reducing the temporal resolution of the operational profile. Normally the worst-case climate scenario is studied, with few sensitivities. Although the annual energy demand is not severely affected, the installed capacities see an increase due to higher peak demands in the system. However, there is little literature in an integrated approach that takes into account both demand- and supply-side impacts, together with a high temporal resolution. Overcapacity is the common answer to address the new challenges, but no alternative technologies are considered. This paper aims to address the gap in incorporating climate variability in long-term energy planning. It proposes an approach to integrate the impact of climate and weather variations in a capacity expansion planning model and studies their impact on the European energy system planning. A model with selected European countries covering a wide latitudinal range is used to test and study the proposed approach.
This paper splits in six following sections. Section 2 reviews some of the key concepts in energy system and climate modeling. Section 3 determines the main climate parameters to consider and discusses the process of the climate data collection and processing. The modeling and analysis of the impact of the climate variables is presented in section 4 for the electricity demand and in section 5 for the generation and transmission. The conclusions and further implications are discussed in section 6.
2. Climate modeling and capacity expansion model
Climate modeling is an important pillar of climate science, which is us ed to study the past and future behavior of the global climate. Regarding the latter, it focuses on projections and analysis of the possible trends that climate parameters will have in the coming decades. The considered assumptions clearly impact the final projections. Different scenarios are created to gather in a standardized wa y several sets of assumptions Emission scenarios are the base for climate modeling. They define different tr ajectories of Greenhouse Gases (GHG) emissions that would be emitted during the next decades according to several assumptions. As there are different stakeholders worldwide performing climate modeling, a reference set of scenarios is essential in order to have a reference to benchmark the different resulting models. Therefore, the International Panel on Climate Change (IPCC) defines a specific set of scenarios for their Assessment Reports (AR). For the Fifth Assessment Report (AR5), the scenarios were called Representative Concentration Pathw ays (RCP) [21]. The main reference is the radiative forcing on Earth by 2100. Radiative forcing can be defined as the change of the net flux of radiative energy through the atmosphere caused by a change of the properties of the atmosphere. The three main scenarios from this report are: the most optimistic RCP2.6, RCP4.5 and the most pessimistic RCP8.5 [22,23]
Having as a reference the emission scenarios defined by the IPCC, several clima te models can be developed by different organizations following the same underlaying assumptions. The Global Circulation Models (GCMs) describe the dynamics of circulation and heat transfer in the planet [1]. S everal of t hese are grouped by t he Coupled Model Intercomparison Project (CMIP) relating each one to the emission scenarios. The GCMs normally cover a global geographical range. However, for local studies of specific regions, these models are downscaled to Regional Climate Models (RCM) RCM). Different projects around the world perform this process for their own regions . Nevertheless, some standardization is still desired as a reference. The World Climate Research Programme (WCRP) established the Coordinated Regional climate Downscaling Experiment (CORDEX) [24, 25], with a goal of advancing in the regional climate downscaling studies. For the European region, the EURO CORDEX project has been largely developed over the last year s and a grid with the projection of climate parameters with a spatial resolution of 11 km by 11 km can be obtained.
A capacity expansion multi vector and multi zonal optimization model was used for studying the impact of the variability of the climate parameters in the long term energy planning process [26]. It is formulated as a linear problem with a defined set of inputs, equality and inequality constraints with the goal to minimize the total cost of the system including the Capital Expenditure (CAPEX) and Operational Expenditure (OPEX). The residual value of investments with a lifetime greater than the optimization horizon is subtracted from the objective value in order not to negatively bias the investments close to the end of the optimization horizon. The hydrogen layer is also used as an alternative energy vector with its own demand and interfaces with the electricity layer, providing additional flexibility against climate variability. In this study, the framework of the capacity expansion model is extended as shown in Figure 1. Using the weather data from the climate model s, different factors will be pre processed and used as new inputs, as will be shown in the following sections. One open question is a feedback from the optimization model to switch between climate model trajectories in case some targets or goals are not being met.
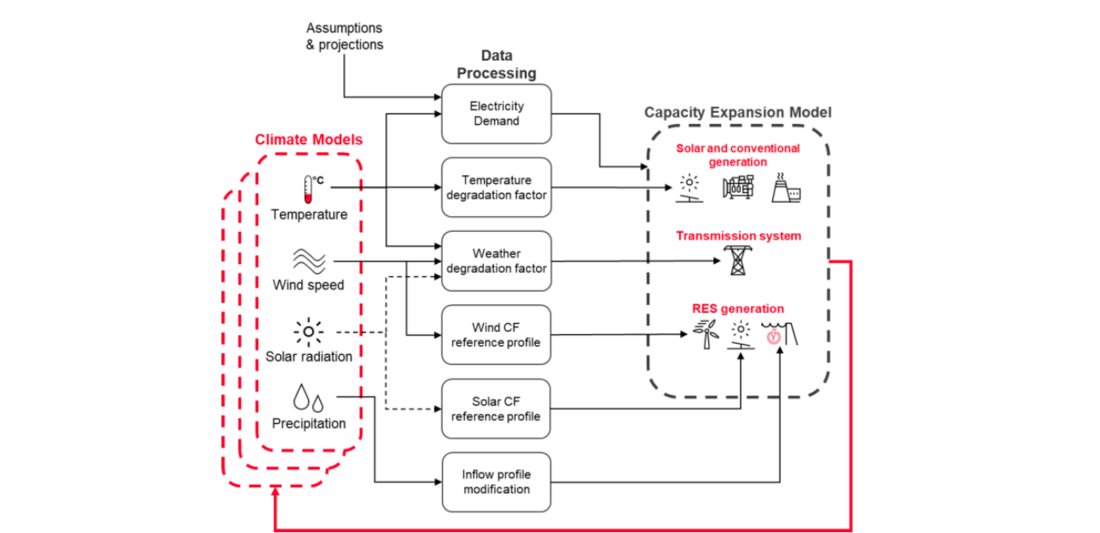
Figure 1 - Extended framework of the capacity expansion model to account for climate impact
For this paper, a reduced European scenario will be used. It is composed by four countries: France, Italy, Switzerland and Great Britain, each represented by one zone. Additionally, seven offshore zones are modeled: two for France and Italy each and three for Great Britain. These countries were sele cted as France, Italy and Great Britain represent a big share of the European electricity demand, and they cover a wide latitude range from the Mediterranean in Italy to the North Sea in Great Britain. This allows to capture the climate and weather dynamics from different l atitudes in the continent. Moreover, the addi tion of Switzerland allows to create a grid topology that is not only in ser ies between the countries.
3. Parameter identification, data collection and processing
The Earth’s climate system can be characterized by different parameters such as: air temperature, relative humidity, atmospheric pressure, precipitation, sea level, wind speed, solar radiation, snowfall, among many others. Even though all of them may affect the power system in a way, it is necessary to identify and select the climate parameters that have a more significant impact in the system. In this study, air temperature, wind speed and solar radiation are the relevant climate parameters that are considered. Figure 2 presents and assessment of the impact of these parameters on the different components of the power system, supplemented by precipitation which is considered but not included in the scope of this paper.
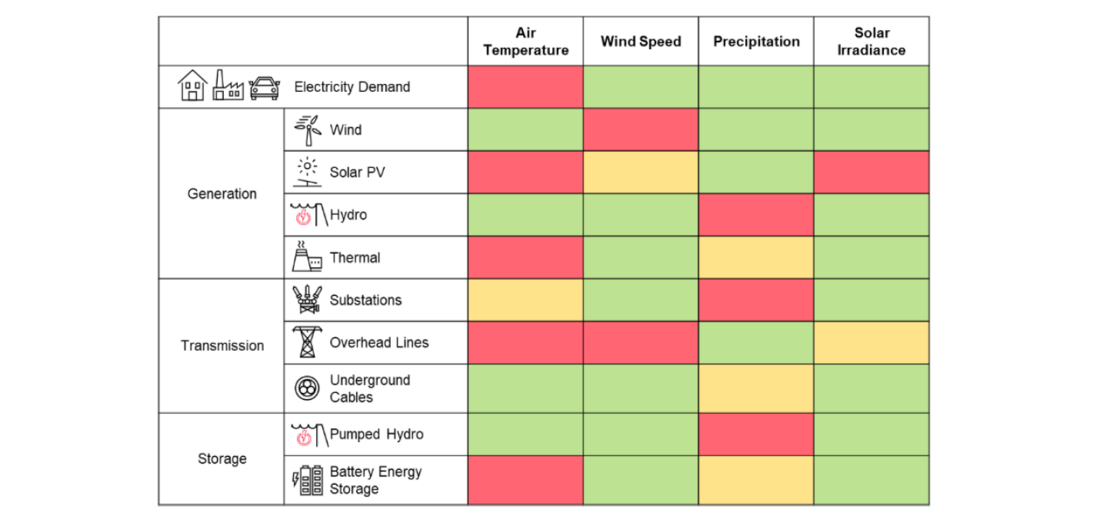
Figure 2 - Impact of air temperature, wind speed, precipitation and solar irradiance on the different components of the power system. Red denotes high impact and green low impact
Air temperature has proven to be one of the main factors affecting the electricity demand profile due to the correlation with the use of HVAC systems in buildings and EVs, which is important for a future where the road transport will be fully electrified. At the same time, air temperature has also been related with the technical performance of different power generation and transmission equipment. Wind speed and solar radiation play a direct role in the VRES units which non-dispatchability depends mainly on these climate parameters. It is a common practice to use one fixed profile, or in some cases multiple, of reanalysis data to try to better represent the historical behavior and dynamics of these parameters. However, it is also important to account for the future variability of them.
3.1. Data collection
The time series of the projections of air temperature, wind speed and solar radiation are defined as a new input for the capacity expansion model and are also required for the demand estimation process. They are downloaded from the CORDEX project database through the interface of the Infrastructure for the European Network for Earth System Modeling (IS-ENES), Climate4Impact. As this study focuses on the European region, that EUR-CORDEX database is used. The spatial resolution of the data is a grid of 11 km by 11 km and the temporal resolution is 3 hours. As the capacity expansion model works with input profiles in an hourly basis, further processing needs to be done to the downloaded data.
For this study, the climate models from the AR5 RCP scenarios are considered over the SSP scenarios from AR6 due to data availability in the Climate4Imapct interface at the moment of downloading the data. Although the three scenarios, RCP 2.6, 4.5 and 8.5 are considered, the RCP4.5 scenario is selected to be the base scenario for this study as an intermediate between the more optimistic (RCP2.6) and more pessimistic (RCP8.5) case. For comparison reasons two climate models will be considered for this paper. The RCA4 RCM from the Swedish Meteorological and Hydrological Institute (SMHI) is used as it is one of the few publicly available datasets. However, one of the models is based on the GCM developed by the Norwegian Climate Center (NCC) called Nor-ESM1-M and the other one is based on the GCM developed by the Max Planck Institute (MPI) called MPI-ESM-LR.
3.2. Data processing
Each downloaded file contains the 3-hour data profiles related to one climate parameter for a specific carbon emission scenario. The first step consists in a geographical processing of the data. Each data point is associated to a set of coordinates (latitude and longitude), which is used to determine if the point lies within the country or countries of interest, in order to get all the points related to the countries in the study. Figure 3a shows an example of the geographical filtering of the air temperature data for France. However, in the zonal capacity expansion model that is used, each country is represented by one zone. For this reason, a unique representative parameter value needs to be determined for each hour of the time series for each country.
The spatial processing of each climate parameter has to be addressed separately, as the way they are distributed over the countries varies. For the air temperature, it is assumed that the largest effect will be on the electricity demand. For this reason, this parameter is processed using a population-weighted average. The main urban centers of each one of the countries are identified and their populations and surface areas are recorded. The population determines the weight of the urban center in the country average while the area determines the number of data points to be used for the urban center value. Figure 3b shows an example for France, where the main urban centers can be noted. Paris, being the largest one by area, is represented by the largest number of points, while smaller ones as Nice and Strasbourg are only represented by a few of them. Regarding the wind speed and solar radiation, there are two approaches that can be taken. The first one is to calculate the simple average of all the points inside the country, but this could lead to sub or over estimation of these resources. As an alternative approach, the points closer to areas where current installations of these units are located would be used for the country’s representative value. These locations can be taken from databases as Wind Europe for the density of installed capacity of wind power [27].
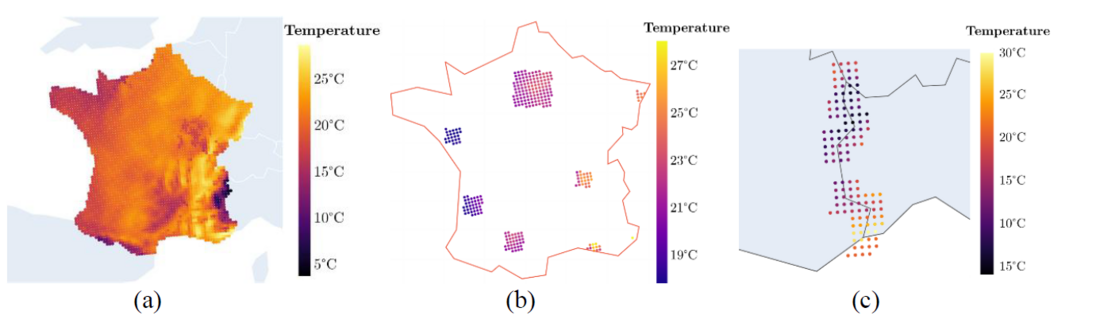
Figure 3 - (a) Geographical filtering, (b) processing of the air temperature data for France considering the main urban centers in the country and (c) data filtering for interconnectors
As it will be presented in section 5.2, the transmission grid is affected by all three climate parameters which are used in this study. As the location of the transmission lines between the different countries vary in each case, the countries’ representative value cannot be used in this case. For this reason, a simple average approach is used, but with points which lie along the border of the two countries to be considered. Figure 3c shows an example for the border between France and Italy.
3.3. Interpolation, morphing and hub height
After the geographical processing, a representative profile for each country and cross-border interconnection is obtained. However, the temporal resolution of these profiles is still the 3 hours that the original profiles had. A linear interpolation is used to generate an hourly profile for each one of the climate parameters. As the investment step used in the capacity expansion tool is 5 years, a 5-year average is calculated for each investment step. As it is shown in equation (1), the years that are taken into account are from two years before until two years after the investment step year.
(1)
Other aspect that needs considered is the uncertainty of the climate models with respect to the actual observations. For this reason, a morphing process [28] of the retrieved data from the climate model is carried out. This consists of calculating the variation of the parameters’ value for each investment step relative to the reference point of 2020, as shown in (2). Afterwards, this variation is added to the actual value recorded for 2020, as shown in (3) using the reanalysis data of Renewable Ninja.
(2)
(3)
Finally, the wind speed that is retrieved from the climate model is at a height of 10 m. This value cannot be directly used as it would considerably underestimate the wind potential. The average hub height of current wind turbines has already passed 100 m. Therefore, it is necessary to estimate the wind speed at these heights in order to correctly calculate the wind potential. For this purpose, the wind speed profile logarithmic law is used, as it accurately describes the wind speed profile distribution up to a height of 100 m. For this study a surface roughness of 0.05 m is used, corresponding to agricultural land with some crops and properly separated small buildings.
4. Impact on electricity demand
The electricity demand is heavily influenced by the air temperature as shown by different literature. In the framework of this study a correlation analysis between the electricity demand and the air temperature is performed to verify this correlation. France and Italy are selected as they can be positioned in two different latitudes and heating/cooling trends. The electricity demand is retrieved from ENTSO-E Transparency Platform and the population-weighted average of air temperature from Renewable Ninja are used. There are different patterns of consumption for weekdays and weekdays; weekdays are selected as they represent the largest portion of the week and are a close representation of business as usual. Figure 4 shows the correlation between electricity consumption and air temperature for France and Italy. It can be observed that the points follow a U-shape pattern. The left side of the curve represents the increase in demand due to heating units, while the right side corresponds to the usage of cooling devices. Even though the range and slope of the curves vary per country/latitude, the inflection point occurs at the same temperature between 17°C and 20°C. Each one of the sides of the curve can be treated as a linear function starting from defined temperature setpoints. It is then validated the dependency of the electricity demand with the air temperature.
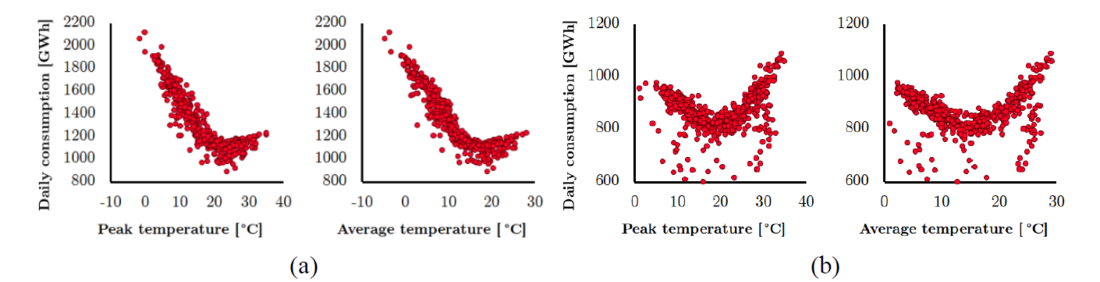
Figure 4 - Daily electricity consumption correlation with the peak and average temperature of (a) France and (b) Italy for the years 2018 and 2019
4.1. Demand Modeling
In order to correctly study the impact of the air temperature in the electricity demand a bottom-up approach is necessary as the impact on the different end-use sectors vary. For this paper the impact on the buildings and transport sector is considered. From the literature, and similarly to the electricity demand analysis performed in this paper, the buildings space heating demand can be modeled as a linear function dependent on the air temperature. As there is a range for thermal comfort, Heating Degree Days (HDD) and Cooling Degree Days (CDD) are used for the calculation. They are defined as the difference between the average daily temperature and the setpoint temperature for heating and cooling, and then the result from each day is aggregated.
As a standardized approach is desired, the heating demand per capita is intended to be parametrized in function of the HDD. For this matter, the heating energy demand is retrieved for different countries in Europe for the year 2019 and then divided by the population. A regression of the correlation of each one of these points with the number of HDD that the respective country experienced during the year was performed resulting in equation (4). It is assumed that the heating demand for commercial buildings is proportional to the residential one, using the floorspace of each building stock as the ratio between them.
(4)
For the cooling energy demand, the approach by [12, 13] is used. These identify that the residential buildings also follow a linear function, but the commercial buildings follow an exponential function. However, another factor that needs to be considered is the share of buildings stock that uses the air conditioning system, also as a factor of the CDD.

These relationships can be used to estimate the energy demand for space heating and cooling. The required inputs to perform this process for every country are: floorspace, population. Then the electricity demand can be estimated using the assumed electrification share and efficiency of heating units e.g., heat pumps. The annual value is converted to an annual hourly profile by using the distribution of Heating/Cooling Degree Hours (HDH/CDH), as shown in equation (5). They follow the same definition as the HDD and CDD, but they don’t aggregate the daily number but refer to the difference in temperature for every hour. The same process of equation (5) is followed for the cooling demand. The additional subsectors of the building sector i.e., appliances & lighting, cooking, etc. are added to the space heating and colling profiles to get the total buildings electricity profile.
(5)
For the transport demand, the forecast of the driving distance of the road EV fleet and the electricity consumption per km are considered [14]. The air temperature impact is included by considering the share of the stored electricity in the battery that is used for running the heating system (HSB), which is defined in equation (6). It can be assumed that the electricity that is required to run the heating system is additional electricity that will be charged to the battery. Therefore, the calculated demand profile for EV can be increased by the HSB factor. The other means of transportation electricity profiles are not considered to be affected by variation in the climate parameters. Consequently, their calculation is not modified. The industry sector demand profile is also assumed to remained unchanged.
HSB[%] = – 0.674 · T + 19.088 (6)
4.2. Demand projections
After downloading the air temperature data sets and processing them, the electricity demand was calculated for each sector. The base scenario considers a RCP4.5 scenario. The climate model used is from the “EUR-11_NCC-NorESM1-M_rcp45_r1i1p1_SMHI-RCA4_v1” project. As an example, Figure 5a shows the processed temperature profile for France for the investment steps of the capacity expansion model. It can be observed that there is an increase in the average and peak temperatures. The average temperature increases from 12°C to 13.1°C, while the peak temperature increases from 23.2°C to 25.9°C. Another example is Great Britain, where the average and peak temperature increase from 10°C and 18.7°C to 10.9°C and 20.7°C, respectively. It can also be visually noted that the curves for the investments steps farther in the future is above the present years during most of the year. Additionally, in Figure 6a and Figure 6b is evident how the number of HDD decrease and the number of CDD increase along the time, confirming warmer winters and summers leading to a variation in the energy demand patterns.
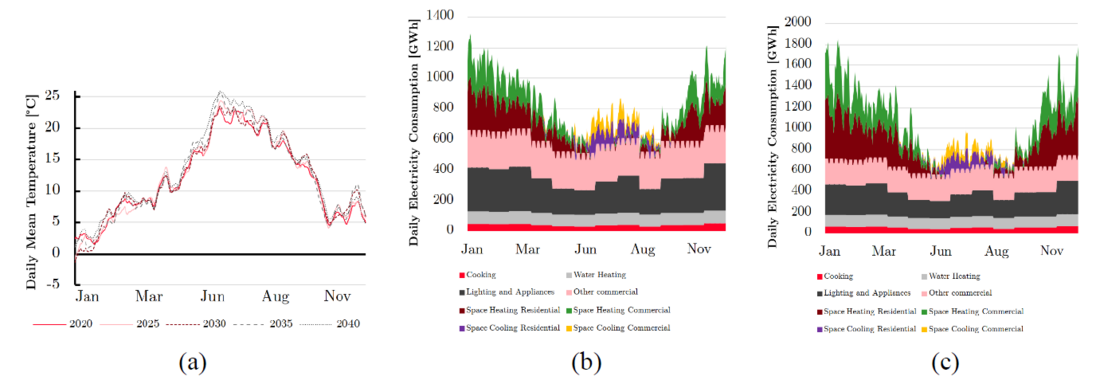
Figure 5 - France (a) 14-day rolling daily mean temperature and buildings electricity daily consumption for (b) 2025 and (c) 2040
Focusing on the electricity demand of the buildings sector, it will present an increase driven by the increased electrification share of the heating demand and higher peak temperatures during the summer season. Figure 5b presents a daily electricity consumption profile for the different subsectors of the building sector in France for the investment step of 2025, while Figure 5c does for 2040. For winter, the peak daily consumption in 2025 is 1,292 GWh, while it increases to 1,852 GWh in 2040. Likewise, during summer the peak increases from 868 GWh to 985 GWh. The space heating and cooling subsectors also increase the annual consumption from 75 TWh and 14 TWh to 132 TWh and 18 TWh, respectively. This represents an increase of 76% for space heating and 28% for space cooling.
To emphasize on the importance of considering more than one climate model projection when performing long-term energy planning, the base case demand projections are compared to a sensitivity case where the driving GCM is the MPI_ESM_LR model, instead of the NorESM1-M from the base scenario. Figure 6shows the main differences in the estimated values. Even though the number of HDD also decrease along the horizon with the new model, it is generally a lower value and follows a different trend with a sharp decrease from 2030 to 2035, compared to the similar behavior from 2035 to 2040 in the base scenario. The CDD present a different pattern, as they don’t increase as such as in the base scenario. In the MPI model they have an increase in 2030, but afterwards they go back to a lower level. Regarding the total electricity demand, Figure 4c compares this variable for France for both models. It can be noted that the demand for the new climate model is lower for most of the investment steps. In the last investment step, it is reduced from 581 TWh to 574 TWh.
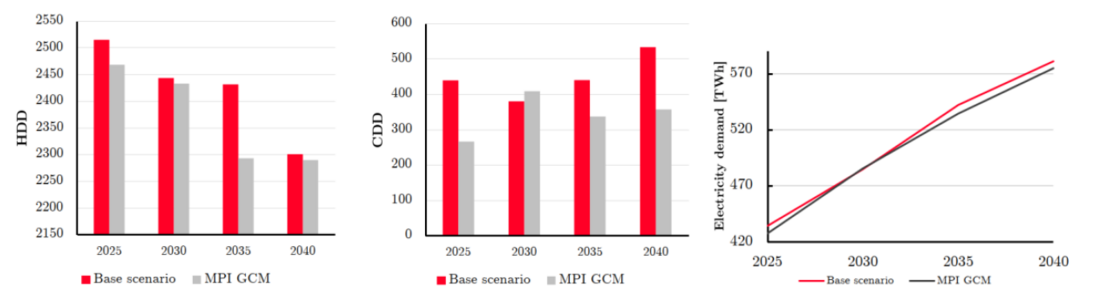
Figure 6 - France forecast of (a) HDD, (b) CDD and (c) electricity demand
5. Impact on generation and transmission
The generation fleet of a power system can be affected by different climate and weather parameters. First of all, the variable renewable (VRES) generation is directly affected by the corresponding climate parameter or renewable source; wind power is affected by the wind speed and solar power by the solar radiation. The output of a wind power turbine is characterized by the wind power curve, which consists of four zones: (1) zero output when the wind speed is lower than the cut-in wind speed, (2) P u between the cut-in and rated wind speeds, following the power curve, (3) the rated power output power between the rated and cut-off wind speeds, and finally (4) zero output when the wind speed is larger than the cut-off wind speed. Regarding the solar power production, its generation proportional to the solar radiation. However, its output is also affected by the air temperature. It is reported that the maximum output and the efficiency of the solar panels are reduced by 0.66% and 0.08%, respectively, per each Celsius degree above a reference temperature of 25°C [18, 20].
The conventional generation units are also affected by the air temperature. They are machines that have a defined operating temperature range. When the air temperature goes beyond a specified reference temperature, then the cooling capability of the generator units is compromised and the output capacity is reduced. Both air-cooled and water-cooled generator units are affected. It can be stated that per each Celsius degree that the air temperature increase, the cooling water of a conventional power plant will increase its temperature by 0.8°C [20]. The impact of the air temperature on the maximum power output and efficiency depends on the type of generator. Table 1 summarizes these values for different unit types [18].
| Affected variable | Generator | Effect from coolant temperature | Effect from air temperature | Reference temperature |
|---|---|---|---|---|
| Maximum output capacity | Solar PV | - | 0.66% / °C | 25°C |
| Nuclear | 0.4% / °C | 0.32% / °C | 15°C | |
| NGCC | - | 0.4% / °C | 15°C | |
| Efficiency | Solar PV | - | 0.08% / °C | 25°C |
| Nuclear | 0.12% / °C | 0.1% / °C | 15°C | |
| NGCC | 0.27% / °C | 0.21% / °C | 15°C | |
| Gas | 0.24% / °C | 0.19% / °C | 15°C | |
| Coal | 0.17% / °C | 0.14% / °C | 15°C |

The electrical grid network is also affected by several climate parameters as the overhead lines are exposed to all climate conditions. The system variable that is mainly concerned is the line ampacity i.e., maximum transmission capacity, which is defined by the heat balance of the conductor. The Joule heat is defined by the line current (I) and the resistance of the conductor (R), which is temperature dependent. The heat gained from the solar radiation is dependent on that specific climate parameter δ )). The heat loss by radiation
is also dependent on the air temperature. And finally, the heat loss by convection
is a function of the wind speed (u) and air temperature. Equation (7) defines the ampacity of the line, assuming a maximum conductor temperature of 80°C.
(7)
5.1. Generation modeling
The capacity expansion model that is being used has a set of equality and inequality constraints that define the problem. For the VRES generation units the power output profile is defined as the multiplication of the installed capacity with a reference standardized (range 0-1) profile. As of now, the input for this profile was reanalysis data from Renewables Ninja, which was repeated for each one of the investment steps. In this study the reference profiles are generated by using the associated climate parameters i.e., wind speed and solar radiation. The wind reference profile is generated following the wind power curve. The function P(u) for the zone 2 is calculated as a 9th-grade polynomial expression. Regarding the solar reference profile, it is generated by proportionally following the solar radiation profile. A proportional factor of 0.00092 m²/W is used to create the dimensionless profile.
The impact of the air temperature on the generation units’ output is also modeled and inserted into the optimization model. Both for the solar power and the conventional generation units a temperature efficiency is defined as in equation (8). For the efficiency or power output loss the values are taken from Table 1, while k denotes for the heating ratio of the coolant relative to the air, which was discussed to be 0.8. This temperature efficiency is later introduced in the constraints of the generation units. For the solar PV it is introduced in the power profile constraint, while for thermal generation it is introduced in the upper-bound limit capacity constraint.
(8)
5.2. Transmission modeling
It was explained that the OHL ampacity can be described as in equation (7). However, given the linear formulation of the problem, it cannot be directly introduced as a constraint. Instead, a ratio between the estimated ampacity profile and a reference line ampacity of 2,000 A is considered. This process is performed exogenously to the model and results in a vector with these ratios (denoted climate efficiency), which is later inserted into the upper-bound line capacity constraint.
5.3. Optimal investment mix
The capacity expansion tool is run for different configurations. For this paper two cases are presented using the demand projections shown in section 4.2: the reference case which does not consider climate impact, and a case study where climate impact is considered. Figure 7 presents the required new capacity investments in the different technologies for both scenarios, while Figure 8 shows the annual electricity generation of the different sources. These results are for all the zones of the case study model.
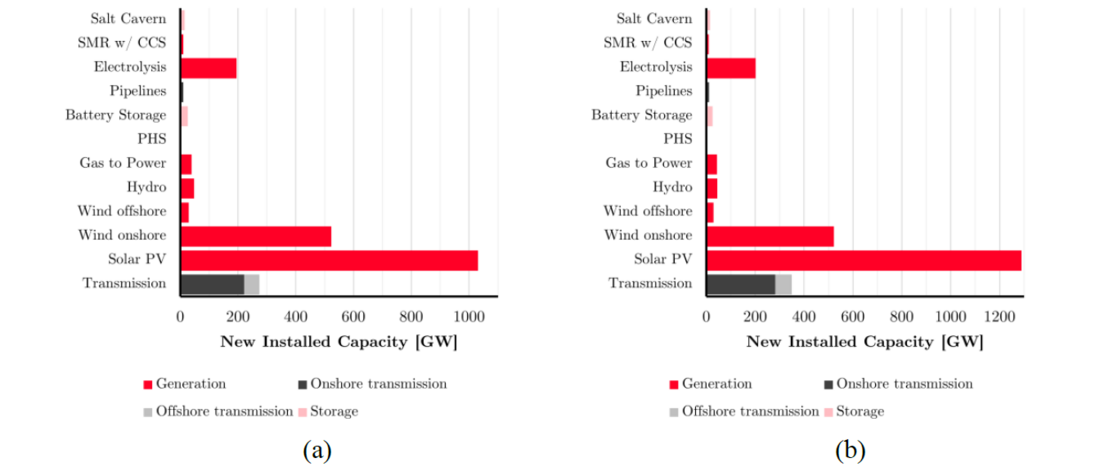
Figure 7 - Optimizer output of cumulative new installed capacity (a) without considering climate impact and (b) considering climate impact
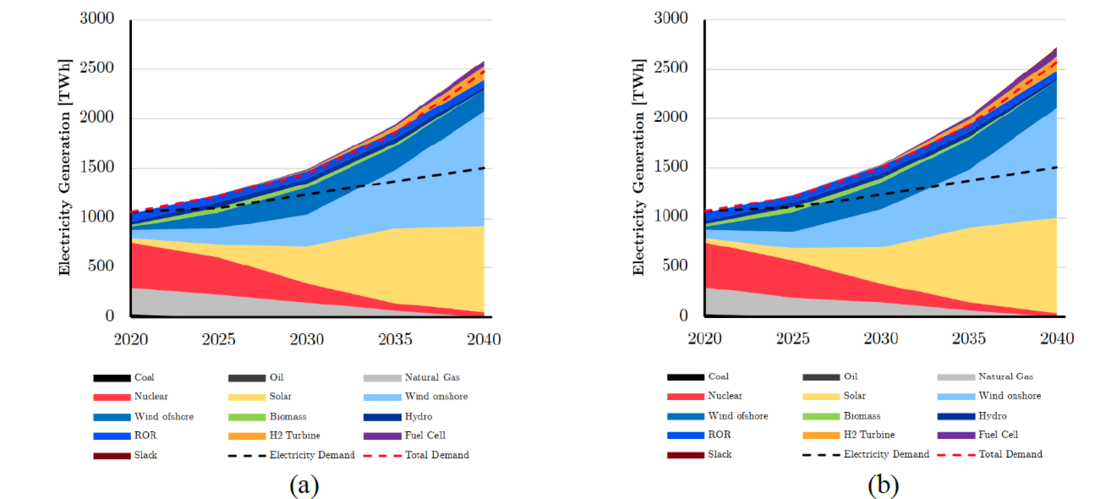
Figure 8 - Optimizer output of annual electricity generation evolution (a) without considering climate impact and (b) considering climate impact
It can be noted that there are several variations both in new installed capacity and annual electricity generation between both cases. However, it is good to disclose that both with and without climate impact the onshore wind power capacity is limited by an investment step limit. This is introduced in the model to account for supply chain and production restrictions. It constrains the maximum new capacity investment in a determined step as a percentage of the installed capacity of the previous step. As a consequence, the installed capacity of onshore wind remained unchanged when the climate impact is introduced. Nevertheless, given the variability of the wind resource, the annual electricity generation sees a small variation. It is reduced by 3% from 1,157 TWh to 1,115 TWh. Offshore wind also sees no change in the installed capacity, but an increase in electricity generation of 24% from 221 TWh to 275 TWh, indicating more favorable offshore wind conditions when using the climate forecasts. The battery storage units are also constrained by the investment step limit. As these three resources are limited by the investment step limit, the additional requirements should come from other technologies.
One variable that also experience a change is the electricity demand for running electrolyzers and producing hydrogen. It increases by 10% from 968 TWh to 1,065 TWh when considering the climate impact. The capacity of the electrolyzers is not changed, but their utilization increases. In this way, given the limitations for the electrical storage, hydrogen is also used as a flexibility resource. However, this additional required electricity must be produced by new installed capacity of one of the technologies. This is the case of solar power, which is not limited by the step investment limit. The installed capacity increases by 25% from 1,031 GW to 1,290 GW, while the annual electricity generation in the last investment step of 2040 is increased by 11% from 866 TWh to 963 TWh, when the climate impact is considered. Finally, the transmission network also sees an increase of 10% in its transmission capacity from 221 GW to 282 GW. This can be explained both by the impact from the climate parameters, which reduce the line ampacity and hence a larger installed capacity is needed, and also by the location of the new solar installed capacity, which can be located in regions with better solar resource and delivered to the load centers.
6. Conclusion & outlook
It is established that the variability of climate and weather parameters has an impact on different components of the energy system; from de demand- and supply-side, as well as the transmission network. The electricity demand is found to be dependent on the air temperature through the calculation of HDD and CDD. However, the level of electrification of the space heating sector also plays an important role. Even though the number of HDD is reduced in the following years, the electrification of the heating sector will increase its electricity demand. The type of electric heating units used influences the average efficiency of the sector. Therefore, it is crucial that research is kept undergoing for increasing the Coefficient of Performance (COP) of heat pumps, so even if the space heating demand increases due to some temperature spikes, the electricity demand would not do it at the same rate.
Average and peak temperatures of the different countries will increase in the future. This will lead to a higher number of CDD, which consequently increases the electricity demand for space cooling. One aspect that was not included in this study but should be taken into account is the thermal efficiency of the building stock. It is expected that in the future buildings will be more efficient and will require less energy to heat up or cool down the indoor temperature to a human comfort zone.
Regarding the power generation units, they will also be affected by the variation of climate parameters. The wind speed, solar radiation and air temperature will affect the supply-side. In the near future, the variation in air temperature will affect the output of the conventional thermal generation units. However, when performing long-term planning, the variability of the VRES will play a bigger role. It was evidenced how by introducing the forecasts for the different years in the future, the energy yield of the variable renewable sources, like wind, can change without modifying the installed capacity. And the change in these patterns could lead to a higher requirement of energy storage and consequently generation to supply the affected hours. The step investment limit is also found to be a limiting factor in different scenarios. Although it is a constraint that should be considered to model the real-life capability of deployment and commissioning of technologies, it is also a warning to evaluate current policies and estimates of production capability and how they can be improved.
Finally, this paper established an integrated approach where the impact of the climate change, and the inherent variability of related climate and weather parameters, on the different components of the power system is assessed using a capacity expansion optimization tool. In the framework of this paper, only long-term climate projections were used. It was assumed that they already include forecasted increased frequency and intensity of extreme weather events. Future work is expected using a similar integrated approach, considering all components of the power system, but simulating scenarios with synthetic more frequent and severe weather events to test the performance and limits of the systems under stress.
References
- A. M. Brockway and L. N. Dunn, "Weathering adaptation: Grid infrastructure planning in a changing climate," Climate Risk Management, vol. 30, p. 100256, 2020.
- J. Ciscar, D. Ibarreta, A. Soria and L. Feyen, "Climate impacts in Europe: Final report of the JRC PESETA III project," EU Joined Research Center, 2018.
- M. Auffhammer, P. Baylis and C. H. Hausman, "Climate change is projected to have severe impacts on the frequency and intensity of peak electricity demand across the United States," Proceedings of the National Academy of Sciences of the United States of America, vol. 114, no. 8, pp. 1886-1891, 2017.
- L. Clarke, J. Eom, E. H. Marten, R. Horowitz, P. Kyle, R. Link, B. K. Mignone, A. Mundra and Y. Zhou, "Effects of long-term climate change on global building energy expenditures," Energy Economics, vol. 72, pp. 667-677, 2018.
- S. Murphy, L. Lavin and J. Apt, "Resource adequacy implications of temperature-dependent electric generator availability," Applied Energy, vol. 262, 2020.
- F. Song, Y. Wang, L. Zhao, K. Qin, L. Liang, Z. Yin and W. Tao, "Study on thermal load capacity of transmission line based on IEEE standard," Journal of Information Processing Systems, vol. 15, no. 3, pp. 464-477, 2019.
- Z. Khan, G. Iyer, P. Patel, S. Kim, M. Hejazi, C. Burleyson and M. Wise, "Impacts of long-term temperature change and variability on electricity investments," Nature Communications, vol. 12, no. 1, 2021.
- A. N. Stevens, "Factors Affecting Global Climate," Nature Education Knowledge, vol. 3, no. 10, 2011.
- L. Wenz, A. Levermann and M. Auffhammer, "North–south polarization of European electricity consumption under future warming," Proceedings of the National Academy of Sciences of the United States of America, vol. 114, no. 38, pp. E7910-E7918, 2017.
- S. Avdakovic, A. Ademovic and A. Nuhanovic, "Correlation between air temperature and electricity demand by linear regression and wavelet coherence approach: UK, Slovakia and Bosnia and Herzegovina case study," Archives of Electrical Engineering, vol. 62, no. 4, pp. 523-532, 2013.
- M. Berger and J. Worlitschek, "A novel approach for estimating residential space heating demand," Energy, vol. 159, pp. 294-301, 2018.
- M. Jakubcionis and J. Carlsson, "Estimation of European Union residential sector space cooling potential," Energy Policy, vol. 101, pp. 225-235, 2017.
- M. Jakubcionis and J. Carlsson, "Estimation of European Union service sector space cooling potential," Energy Policy, vol. 113, pp. 223-231, 2018.
- M. Steinstraeter, T. Heinrich and M. Lienkamp, "Effect of low temperature on electric vehicle range," World Electric Vehicle Journal, vol. 12, no. 3, 2021.
- M. Bartos, M. Chester, N. Johnson, B. Gorman, D. Eisenberg, I. Linkov and M. Bates, "Impacts of rising air temperatures on electric transmission ampacity and peak per-capita electricity load in the United States," Environmental Research Letters, 2016.
- K. Solaun and E. Cerdá, "Climate change impacts on renewable energy generation. A review of quantitative projections," Renewable and Sustainable Energy Reviews, vol. 116, 2019.
- L. Wei, L. Jiheng, G. Junhong, B. Z. F. Lingbo and H. Baodeng, "The Effect of Precipitation on Hydropower Generation Capacity: A Perspective of Climate Change," Frontiers in Earth Science, vol. 8, 2020.
- M. R. Allen-Dumas, B. KC and C. I. Cunliff, "Extreme Weather and Climate Vulnerabilities of the Electric Grid: A Summary of Environmental Sensitivity Quantification Methods," Oak Ridge National Laboratory, 2019.
- A. Miara, S. M. Cohen, J. Macknick, C. J. Vörösmarty, Y. S. Fabio Corsi, V. C. Tidwell, R. Newmark and B. M. Fekete, "Climate-Water Adaptation for Future US Electricity Infrastructure," Environmental Science and Technology, vol. 53, no. 23, pp. 14029-14040, 2019.
- P. Dowling, "The impact of climate change on the European energy system," Energy Policy, vol. 60, pp. 406-417, 2013.
- IPCC, "Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change," Geneva, 2014.
- R. Moss, J. Edmonds, K. Hibbard, M. Manning, S. Rose, D. Vuuren and others, "The Next Generation of Scenarios for Climate Change Research and Assessment," Nature, vol. 463, pp. 747-756, 2010.
- D. P. van Vuuren, J. Edmonds, M. Kainuma, K. Riahi, A. Thomson, K. Hibbard and others, "The representative concentration pathways: an overview," Climatic Change, vol. 109, 2011.
- D. Jacob, C. Teichmann, S. Sobolowski and others, "Regional climate downscaling over Europe: perspectives from the EURO-CORDEX community," Regional Environmental Change, vol. 20, p. 51, 2020.
- F. Giorgi and W. J. Gutowski, "Regional Dynamical Downscaling and the CORDEX Initiative," Annual Review of Environment and Resources, vol. 40, 2015.
- K. Knezović, A. Marinakis, C. Evrenosoglu and A. Oudalov, "Role of grid and bulk storage in the integration of variable renewable energy resources: Framework for optimal operation-driven multi-period infrastructure planning," Energy, vol. 226, p. 120378, 2020.
- Wind Europe, "Map of onshore wind farms," Wind Europe, 2021. [Online].
- S. E. Belcher, J. Hacker and D. Powell, "Constructing design weather data for future climates," Building Services Engineering Research and Technology, vol. 26, 2005.

