C4 - Transformer withstand capability to temporary overvoltages: a general determination method from standard data
Author
Manuel MARTINEZ-DURO - EDF, France

Summary
Temporary overvoltages (TOV) are power frequency overvoltages of relatively long duration. They can originate from several causes: earth faults, load rejection, fault clearing, transformer energization, etc. TOV generate both dielectric and thermal stresses that may damage the equipment.
The problem is that there is very little information on transformers withstand capability to TOV. According to IEC 60071 standard on insulation coordination, in order to check the dielectric capability of the equipment to TOV the standard withstand voltage test is the “short-duration power frequency test”. However, these tests do not cover all the problems related to TOV, for a number of reasons: the power transformers may see TOV of higher amplitudes although of shorter duration than those of the dielectric tests; the TOV may not be purely sinusoidal but may contain harmonics; the power transformers are submitted to ageing, thus the dielectric withstand may have been reduced over time; the dielectric tests do not cover the thermal effects of the overfluxing generated by the TOV. Some international working groups have provided “typical” voltage-time curves where the voltage withstand capability is given as a function of time, but most of these curves account only for the overfluxing phenomenon. Moreover, these curves are given for purely sinusoidal power-frequency overvoltages of a given amplitude, without any indication of how to use them in the general case of time-varying amplitude. Anyhow, it is doubtful that a unique curve can be representative of all the transformers, given the huge differences in internal design and in the dielectric tests carried out and their voltage levels.
The goal of this paper is to present a transformer TOV capability determination method, for which only standard available data is needed, which accounts for the following key factors: the interdependence between the withstand amplitude and the duration, the fact that the amplitude of the actual overvoltages is time-varying, the presence of harmonics and the insulation ageing.
Keywords
Overvoltage withstand, Transformers, TOV1. Introduction
Temporary overvoltages (TOV) are power frequency overvoltages of relatively long duration, more precisely their frequency is between 10 and 500 Hz and their duration between 20 ms and 1 hour [1]. They can originate from several causes [2][3]: earth faults, load rejection, fault clearing, transformer energization, compensated line resonance due to uneven breaker pole operation, resonance in double-circuit compensated lines, switching of inductive and capacitive currents, etc.
In general, for phase-to-ground TOV lasting a few seconds or less, the surge arresters connected between phase and ground to protect the transformers from switching and lightning surges are the most vulnerable equipment; however, for longer durations, the most vulnerable equipment to phase-to-ground TOV generally are the power transformers [3][4]. Regarding phase-to-phase TOV, as surge arresters between phases are seldom used, three-phase power transformers are usually the most vulnerable equipment.
The TOV can damage transformers due to two different physical phenomena: dielectric stress and, for longer durations, thermal stress. On the one hand, TOV can generate a dielectric breakdown if the voltages inside the transformer exceed the dielectric strength of the insulating structures; on the other hand, TOV may generate an overfluxing, which increases the losses and therefore the temperature, which can end up damaging the insulation. In this paper we will deal with dielectric stresses, for which the problems are more acute, but we will also provide some practical indications about thermal effects.
According to IEC 60071 standard on insulation coordination [2], in order to check the dielectric capability of the equipment to TOV the standard withstand voltage test is the “short-duration power frequency test”. For this, the last version of the IEC standard on power transformer insulation levels and dielectric tests [5] defines up to four tests, depending on the rated voltage and the type of insulation, uniform or non uniform: Applied voltage (AV), Line terminal AC (LTAC), Induced voltage withstand (IVW), Induced voltage with PD (IVPD). Each of these tests is made with a constant-amplitude sinusoidal voltage of frequency equal to the power system frequency (50/60 Hz) or a small multiple of it (for instance, 200 Hz). According to the standard on insulation coordination [6], the test withstand voltage amplitudes must be divided by a security factor Ks=1.15. The actual test voltage levels of a specific transformer depend on customer choices; however, a global test voltage around twice the rated voltage can be used as a usual value; applying Ks, this leads to an overvoltage withstand around 1.74 times the rated voltage.
However, using this procedure may not be enough to assess the impact of a given overvoltage on a given transformer. There are several reasons for this: first and foremost, the power transformers may see TOV of higher amplitudes, although of shorter duration than those of the dielectric tests. This is for example the case when energizing large power transformers at the end of long lines or cables [9][10], which is a common situation during power restoration or when connecting offshore wind-farms to the grid. Furthermore, the TOV may not be purely sinusoidal but may contain harmonics, what is sometimes called temporary harmonic overvoltages [8]. Also, as the power transformers are submitted to ageing, the dielectric withstand may have been reduced over time.
The problem is that there is very little information on transformers withstand capability to (harmonic) TOV [11][12][13]. Some international working groups have provided “typical” voltage-time curves where the voltage withstand capability is given as a function of time, but most of these curves account only for the overexcitation phenomenon, only a few deal with the dielectric stress [21][22][23]. Moreover, these curves are given for purely sinusoidal power-frequency overvoltages of a given amplitude, without any indication of how to use them in the general case of time-varying amplitude. Anyhow, it is doubtful that a unique curve can be representative of all the transformers, given the huge differences in internal design and in the dielectric tests carried out and their voltage levels.
The goal of this paper is to present a transformer TOV capability determination method, for which only standard available data is needed, which accounts for the key factors we have identified: the interdependence between the withstand amplitude and duration, the time-varying amplitude of the overvoltages, the presence of harmonics and the insulation ageing.
We will only consider oil-immersed type transformers. Also, we will consider that the typical characteristics of the TOV are an amplitude between 1 and 2.5 pu, a duration between one power-frequency period (20 ms at 50 Hz) and 10 seconds and a single low-frequency harmonic component [12]. From a practical point of view, the problem we want to solve is the following: given the voltage curves v(t) at the terminals of a transformer (either simulation results or field measurements), do they exceed the transformer withstand capability?
2. Dielectric withstand capability
The dielectric strength is the ability of the internal structures of the transformer to withstand voltage without breakdown or permanent degradation of the insulation. As we have said, to properly characterize the temporary overvoltage withstand of a transformer, it is necessary to take into consideration the fact that only terminal voltages are known (which are the data provided by simulations or measurements), that the overvoltages have a time-varying amplitude and that they may contain harmonics, and that the transformer insulation is subject to ageing. In the following sections, we will propose an answer to each of these questions, and finally group them together in a global method (see §4).
2.1. Internal dielectric stresses from the terminal voltages: spatial formulation of the dielectric stress
Insulation breakdown or degradation can occur between any two points on the transformer that are at different voltage potentials. However, only the voltages at the transformer terminals are known. Therefore, the first problem to be addressed is the relationship between terminal voltages and internal voltages.
The tank, the magnetic circuit, the structural parts and in general all the non-active metallic parts of the transformer are connected to the ground. All these parts are therefore at zero potential. The points of the transformer at non-zero potential are those of the windings. Of course, during normal operation, the different points of the same winding are at different potentials. Thus, to characterize the dielectric strength of a transformer, it is necessary to study the following stresses and define the associated strength:
- the stress between each point of each winding and the ground;
- the stress between each point of each winding and the other points of the same winding;
- the stress between each point of each winding and the points of the other windings.
It is advisable to be more explicit on the third case, the stress between windings: In a single-phase transformer, this refers to the stress between windings of different rated voltage, e. g. the HV/LV stress in a two winding transformer. In a three-phase transformer, there are more subcases to consider: the stress between windings of different rated voltage of the same phase, HVx/LVx (x indicates the name of the phase A,B,C); between windings of the same rated voltage of different phases (HVx/HVy, LVx/LVy), the stress between windings of different rated voltage of different phases (HVx/LVy).
However, none of these internal voltage distributions are known, only the voltages at the transformer terminals are known. To determine the voltages between each pair of points, we can take advantage of the fact that, at low frequencies, the voltage applied between the terminals of a winding is linearly distributed along its length as a function of the number of turns [23]; in other words, the voltage per turn is the same throughout the winding (this may not be entirely true when the transformer saturates a lot, but finite element simulations that we have carried out show that the assumption is still accurate enough).
Therefore, it is very simple from the voltages at the transformer terminals to compute the voltages in all the points of all the windings (with respect to ground) and between any pair of points of any pair of windings (between points of the same winding, between points of different windings). Given the voltages at the two terminals of a winding, 𝑉𝑡1(𝑡) and 𝑉𝑡2(𝑡), the stress to the ground at any point of the winding is:
(1)
where x is the relative position along the length of the winding, defined in [0,1], x=0 being the coordinate of one of the terminals and x=1 the coordinate of the other terminal.
The voltage stress between two points of the same winding:
(2)
And the stress between two points of two different windings whose terminal voltages are Vw1,t1(t), Vw1,t2(t), Vw2,t1(t), Vw2,t2(t):
(3)
2.2. Internal dielectric withstand capability deduced from standard dielectric tests and the highest voltage for the equipment
Transformers undergo several standard dielectric tests. Among these tests, up to four are performed at power frequency, according to the last version of the IEC standard on power transformer insulation levels and dielectric tests [5], depending on the rated voltage of the transformer and whether its insulation is uniform or non-uniform: applied voltage (AV), line terminal AC (LTAC), induced voltage withstand (IVW), induced voltage with PD (IVPD).
Sometimes the transformer has not undergone one of the IVW tests, but a switching impulse test (SI); in this case an equivalent IVW test voltage can be calculated with a conversion factor [6]. These tests allow us to take the first step in the definition of the withstand capability of a transformer. Indeed, as they are performed with low frequency sinusoidal voltages, we can use the expressions (1)(2)(3) and thus, from the terminal voltages applied or induced during the tests [1], determine the voltages generated in each point of the windings and between each pair of points of the same winding and of different windings. The maximum of the absolute value of these test voltages provides a first temporary overvoltage withstand value. This voltage amplitude is allowed for a duration which is the duration of the test (which generally varies between 5 and 60 seconds depending on the test).
Since the test voltages are sinusoidal, a phasor formulation can be used to facilitate the calculations:
(4)
(5)
(6)
In general, it is more interesting to use all the tests and to take the maximum (for each point and each pair of points) for all the tests. The duration associated with the voltages thus obtained will be the minimum of the durations of the tests used, D. If we include a reduction coefficient kr<1 to account for the effect of the voltage harmonics and the insulation aging (see §2.3), we get:
(7)
(8)
(9)
These withstand characteristics have the form of piecewise linear functions, one-dimensional for the withstand to ground (straight line segments), two-dimensional for the withstand between windings (planar segments). As an illustration, Figure 1 shows, for a 300 MVA 400/24 kV YNd11 single-phase transformer, the withstand voltages of the HV and LV windings to the ground and between the HV and LV windings (for the Y winding, x=0 is the neutral terminal; x=1 is the line terminal), obtained from the levels of the standard LTAC and AV dielectric tests performed on the transformer.
The same procedure can be applied to another standard piece of information on the transformer dielectric strength: its highest voltage for the equipment value, Um [1]. This is the maximum voltage that the transformer can withstand indefinitely, its value being equal to or slightly higher than the rated voltage. Figure 2 shows, for the same transformer, the maximum voltages to ground on the HV and LV windings and the maximum voltages between the HV and LV windings, obtained from Um with the expressions (4)(5)(6). These values are associated with an infinite duration, therefore they provide the “∞” characteristics: 𝑉withstand ∞,winding−ground(𝑥), 𝑈withstand ∞,intra−winding(𝑥1,𝑥2), 𝑈withstand ∞,inter−winding(𝑥,𝑦).

Figure 1 - Withstand voltages to ground in both windings (left) and between HV and LV windings (right), obtained from LTAC and AV tests performed on a YNd11 transformer (for Y winding, x=0 is the neutral terminal; x=1 the line terminal) (peak values)
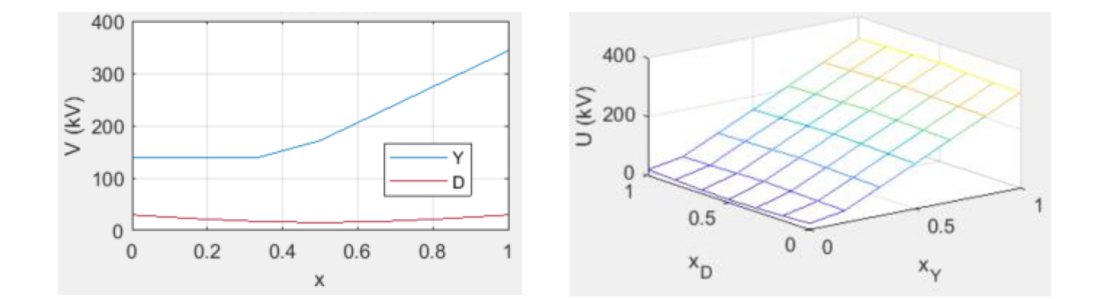
Figure 2 - Maximum voltages to ground (left) and maximum voltages between HV/LV windings (right) from the highest voltage for the equipment, Um, of a YNd11 transformer (peak values)
2.3. Effect of the insulation ageing and of the voltage harmonics
The effect of the insulation ageing and the voltage harmonics will be taken into account by applying a reduction coefficient kr=kageing.kharmonics to the dielectric withstand capability obtained from the standard dielectric tests.
2.3.1. Effect of the insulation ageing
The dielectric withstand capability will decrease over time due to ageing [7]. Three references provide interesting information about this decrease. The standard on insulation coordination IEC 60071-2, addresses this aspect by means of the safety factor, Ks=1.15, which reduces the actual withstand to 87% of the initial value. The IEC 60076-3 standard on transformer insulation levels and dielectric tests states that a repaired or refurbished equipment should have a dielectric strength of at least 80% of the original test levels; this requirement implies that the sound parts of any transformer are assumed to withstand at least 80% of the original test levels. This correction factor applies to all dielectric tests except for the IVPD test, which is not a withstand test but a test to verify the good condition of the transformer insulation; in case of repair, this test must be done at 100% of the initial test level. Finally, the experimental results and the field experience reported in [7] suggest a decrease in the OV withstand due to ageing varying between 5% and 10%, thus a real withstand between 90% and 95% of the initial value. According to these data, we propose using a reduction factor kageing=0.8 for the withstand capability deduced from the dielectric tests, except for the IVPD test.
2.3.2. Effect of voltage harmonics
Temporary harmonic overvoltages are due to the non-linear elements in the power system, mainly power transformers being energized [8]. Whereas multiple current harmonics may be generated, usually there is only one voltage harmonic [21].
Information on the effect of frequency on dielectric strength is scarce. Both [37] and [38] agree that the dielectric strength of oil alone is not frequency dependent, whereas the dielectric strength of solid insulations or oil/solid insulations is very strongly frequency dependent. We propose to use the expression put forward by [37] (reworked in [24]) for the dielectric strength of solid insulations or solid/oil structures: 𝑉(𝑓)/𝑉(60𝐻𝑧)=𝑘/𝑓^𝑛, where V(60Hz) is the withstand voltage at 60 Hz for a given duration, V(f) is the withstand voltage for the same duration at a different frequency f in the range 25 Hz to 500 Hz, and where k and n are constants depending on the type of insulation, with k varying between 1.22 and 1.75 and n between 0.05 and 0.137.
This expression is valid for a purely sinusoidal voltage, but what we are interested in is the dielectric strength to a voltage waveshape that contains a main component at 50/60 Hz and one (smaller) harmonic component. However, we have no information on the global effect of a voltage waveshape with several frequencies. Given this lack of information, we propose to compute an equivalent 50/60 Hz stress (i.e., to be applied to the 50/60 Hz envelope of the voltage waveshape) by assuming a linear combination of the effects of the two frequencies. This is a strong assumption that should be checked against future research on the topic. To be conservative, we will use the value n=0.137. The harmonic component frequency and the relative weights of the fundamental and the harmonic components can be computed by Fourier transform. For example, in the application case shown in §5, the overvoltage has a harmonic component at 300 Hz (for which the expression above gives a reduction factor of 0.78) of 25% relative weight; the resulting reduction factor is then kharmonics=75%*1+25%*0.78=0.95.
2.4. Withstand capability for other amplitudes and durations
So far, the transformer's dielectric withstand capability we have determined corresponds to the amplitudes and durations of the voltages during the standard dielectric tests. For example, for the HV winding, the withstand curve to ground gives, for each point of the winding, a maximum allowable voltage amplitude for a duration that is the duration of the associated test. However, the amplitude of an actual TOV is time-varying, therefore we need to know the withstand capability for other amplitudes and for other durations. The amplitude and duration of the voltage associated with a certain probability of dielectrical failure (partial discharge or breakdown) are directly related: the amplitude determines the duration and vice versa. Several models of this relationship have been proposed [33][36]. In the field of the transformer insulation structures, the most used model is an inverse power law model [33][32]. According to this model, for a given withstand probability, the allowable duration d for a voltage amplitude V>V0 is [25][34][29] :
(10)
where K’P, V0 & n are constants. For voltage amplitudes lower than V0, the allowable duration is infinite.
Thus, given the allowable voltage-durations determined from the dielectric tests, expression (10) can be used to compute the allowable duration for any other amplitude value:
(11)
However, we will not use this expression directly; it will appear implicitly in the expression that gives the probability of failure (see below).
2.5. Withstand capability for time-varying amplitudes
Expression (11) provides the dielectric strength for any amplitude value. However, as the overvoltages seen by a transformer are not of constant amplitude, we need to be able to determine the effect of an overvoltage whose amplitude varies with time. It is important to underline that the dielectric breakdown is not a cumulative energy phenomenon like the thermal phenomena, therefore the effect of amplitude variations cannot be taken into account in the same way as we do for overexcitation or for arresters (see §3).
The natural randomness of the dielectric strength of oil and oil/paper insulation is usually modeled by the Weibull law [33][34][25][35]. If we introduce the inverse power law of the dielectric strength, (10), on the generic expression of the Weibull law, we obtain the following expression of the probability of failure for a sinusoidal voltage of amplitude V and duration d:
(12)
The complementary, 1-PF, provides the withstand probability:
(13)
The parameters n and k are dimensionless; B is a scaling factor; V0 is the voltage below which the allowable duration is infinite.
A fundamental principle of our method is the following: a given overvoltage will be considered allowable, i. e., within the transformer withstand capability, if its associated failure probability PF,OV is less than or equal to the failure probability associated with the dielectric tests, PF,test, i. e. PF,OV ≤ PF,test The value of PF,test is easily computed with the expression (12), from the allowable voltage-durations associated to each of the points and each pair of points of the windings (§2.2). The calculation of PF,OV, is more complex; we propose and compare three alternative methods in the following lines.
Method 1: independent segment contributions
Let V(t) be the voltage we are interested in; {tj, Vj} the N+1 points of the power-frequency envelope of V(t); {dj, Vj} the points that define the N segments of the envelope of amplitude Vj and duration dj= tj- tj-1 .
A first method for determining the probability of failure associated with the overvoltage V(t), PF,OV, is to assume that the probability of failure (or withstand) at each segment j is independent of the voltage that has previously been applied (i. e. the previous segments 1..j-1). In this case, the withstand at each segment {dj, Vj} are independent events, whose probability PW,OV,j can be computed with the expression (13), and the probability that the insulation withstands the whole sequence of N segments, PW,OV, is equal to the product of the probabilities associated with each segment: PW,OV = ∏ PW,OV,j :
(14)
The complementary provides the probability of failure: PF,OV =1-PW,OV = 1-∏ PW,OV,j . The criterium PF,OV ≤ PF,test to determine whether or not the overvoltage exceeds the withstand capability of the transformer, reformulated as PF,OV / PF,test ≤ 1 becomes:
(15)
Remember that V0 is the voltage below which the allowable duration is infinite; for us, it is given by the withstand voltage amplitudes that we have determined from the highest voltage for the equipment, Um (§2.2)
This first method is simple but it has an important drawback. As a matter of fact, if we apply the expression (15) to the amplitude and duration of reference, the result of the ratio should be equal to 1, but it is not. Indeed, if we make Vj=Vwithstand, duration D and dj=d=D/N, the ratio (15) is equal to N1-k. As k<1 (see §2.6), the ratio is greater than 1. In other words, the expression (15) intrinsically overestimates the stress.
In fact, by analyzing the expression of the failure rate associated with the Weibull distribution (not shown here due to lack of space) and taking into account the fact that k<1, it can be shown that the withstand (or failure) at a segment j is not independent of what preceded it, but that a conditioning process occurs [34]. This can be seen in the experimental data. For instance, in the experimental setup for oil gaps in [26] (see Fig. 5) the probability of DP inception for 110 kV applied during 10 seconds is 28%, which corresponds to a withstand probability of 72%; if the effects of successive segments of 10 s were independent, the withstand probability for 1 minute would be 14% (0.726); however, the provided experimental results show that for 1 minute the DPI probability is 59%, which corresponds to a withstand probability of 41%, much higher than the 14% expected under the independence assumption.
In conclusion, the independence method greatly overestimates the stress. Reference [32] investigates an alternative method to account for the conditioning effect, but as the authors' results show, the proposed method may greatly underestimate the stress and thus cannot be employed. In the following lines we propose two alternative methods that try to avoid overestimation without falling into underestimation.
Method 2: independent contributions of groups of similar-amplitude segments
Our analysis of the method 1 shows that, for a constant amplitude Vj=V, considering separately the contribution of each segment {dj, V} leads to an overestimation of the stress compared to considering the whole overvoltage of duration D. This fact suggests an idea for improving the methodology for a general overvoltage {dj, Vj}: to gather all the adjacent segments of similar amplitude and to consider the global contribution of each of these groups of segments, using the total duration of the group and the maximum amplitude in the group. This is illustrated in Figure 3 for a similarity criterium of 5% of the maximum amplitude. Then the expression (15) is applied to the groups. The results in Tableau 2 show that the optimal value of the similarity criterium depends on the considered insulation structure, which is associated to specific Weibull parameter values, n and k (it also depends on the overvoltage waveshape). However, no matter the value of the similarity criterium, the results are always conservative, i. e. they always overestimate the stress, but the overestimation is always smaller than with method 1.
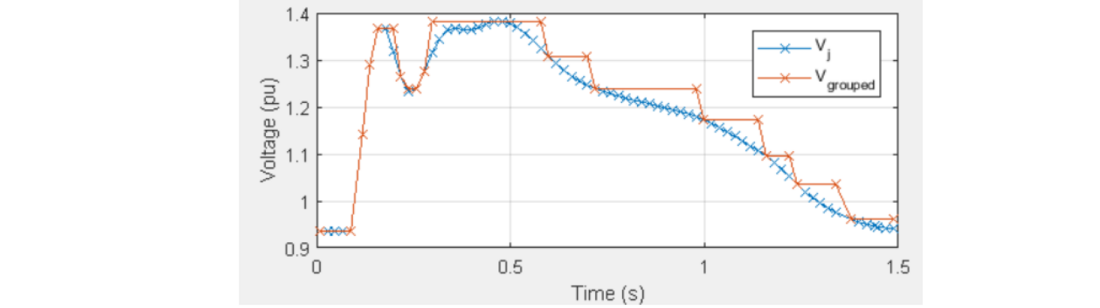
Figure 3 - Groups of adjacent points of similar amplitude (here, 5% range)
Method 3: contributions dependent on the memory effect
The previous methods overestimate the stress, either because they assume independent contributions of the segments {dj, V}, or because they consider the highest amplitude in each contiguous segment of similar amplitude. Here we try to build a method without these two drawbacks. In the general case, the probability that N events (not necessarily independent) occur is given by
(16)
where pj is the probability of the event j, pj|k the conditional probability of the event j when the event k has occurred, pj|(k∩l) the conditional probability of the event j when the events j and k have occurred, etc.
Introducing the definition of the conditional probability, we get:
(17)
For an insulation structure, to withstand an overvoltage made of N consecutive segments {dj, Vj} means to withstand each of the segments one after the another. Thus the withstand probability can be written:
(18)
Let’s consider a voltage of constant amplitude V and duration D, discretized in N segments {dj, V}. As the voltage amplitude is constant, to withstand d1 and d2 and d3 .. dj means to withstand during . Thus
. Let’s call dprev,j the cumulative duration of the previous segments before segment
. We can now write
(19)
The three probabilities in this expression, ,
and
, can be computed with the expression (13). We get then:
(20)
In this expression, the contribution to the withstand probability of each segment {dj, V} depends on the duration associated with the segment, dj, but also on the duration of the previous segments during which the insulation saw the voltage V, dprev,j. Therefore, this term represents the “memory effect” of the dielectric strength, the conditioning effect of the previously applied voltage. Another way of understanding the meaning of the term dprev,j is to cancel its effect: if in expression (20) we make dprev,j=0, we get the expression (14), which provides the withstand probability under the assumption of no conditioning. To cancel the effect of dprev,j is therefore to consider that the effects of the segments {dj, V} are independent, i.e. to eliminate the memory effect.
In the expression (20), the voltage amplitude is assumed constant. To take into account the variation of the amplitude with time, we replace V by Vj. However, if the Vj are no longer equal, the term dprev,j can no longer be calculated as . We will compute this duration which introduces the memory effect in the following way: at each point j, the memory-effect duration will be equal to the duration of the immediately preceding points {dj, Vj} whose amplitude is in the range
, where s will be small enough, for example s=1%. That is to say: the memory effect will be introduced by considering the sequence of previous segments where the voltage was equal to or a little higher than Vj; this sequence stops with the first segment where the voltage is lower than Vj or higher than (1+s)·Vj. This is illustrated in Figure 4. In order not to mix up this new definition with the previous one for the case where the amplitude is constant, we will call this duration dmem,j.
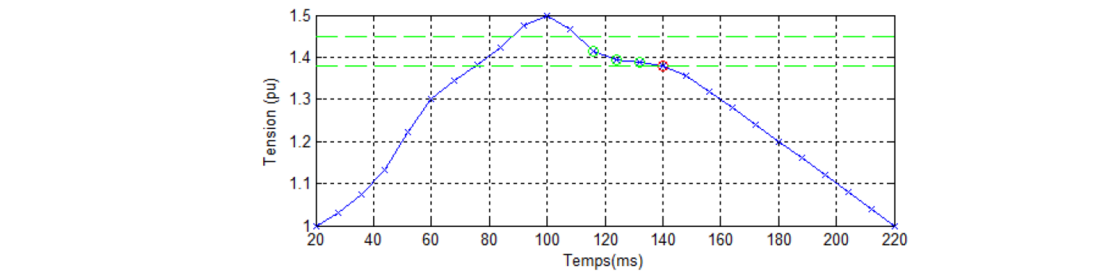
Figure 4 - Computation of dmem,j (point j in a red circle, previous points in the [Vj, (1+s)·Vj] range in green circles)
We are now able to formulate the withstand capability criterium PF,OV,≤ PF,test for time-varying overvoltages:
(21)
This method is somewhat "adaptive": when the amplitude of the voltage is more or less constant (when it remains in the sliding interval [Vj, (1+s)·Vj]), expression (20) takes into account the conditioning effect (memory effect); when the amplitude changes significantly (when it goes out of the sliding interval [Vj, (1+s)·Vj]), the conditioning effect cannot be evaluated and the expression (20) neglects it by considering independently each segment Vj.
Finally, expression (21) can be rewritten in order to define the OV_capability_usage_ratio, a value that indicates how close to (or how far beyond) the withstand limit is the overvoltage:
(22)
The withstand capability of the transformer is exceeded if OV_capability_usage_ratio is higher than 1, i. e. higher than 100%.

2.6. Weibull parameter values to use
There has been a lot of experimental works in other to determine the Weibull parameter values (see expression (12)) for the several types of insulation structures at stake in power transformers: oil gaps, oil duct between barriers, turn-to-turn and coil-to-coil [25]-[36].
Different values are determined for the partial discharge inception (DPI) and for breakdown (BD). The experimental results show that the parameter values are constant if the considered durations are in a given range: short duration (several seconds up to several minutes) or long durations (several hours). We will use the values for DPI for short duration stresses. On the one hand, the temporary overvoltages we are dealing with last several seconds or less; therefore, we will use the values for the short-duration range. On the other hand, the parameter n of the characteristic V-t, expression (10), is much larger for BPI dans for BD; this V-t characteristic is used to determine the withstand amplitudes for durations other than the dielectric test durations (D); the former being shorter than the latter (D varies between 5 and 60 seconds, depending on the considered tests), higher values of n will provide smaller values of V, thus using the values of n for BPI will be conservative. Moreover, this option is consistent with the fact that the dielectric tests don’t lead to BD, but close to BPI.
The Tableau 1 provides the values for the structures oil duct between barriers, turn-to-turn and coil-to-coil; these values are drawn from [29][30] (reworked in [31][32]). For oil gaps [26][27][28] provide a value of n between 12 and 18 (for BD; BPI is not defined for oil gaps).
We have considered three types of stress (§2.1 and 2.2): winding-to-ground, intra-winding, and inter-winding. We need to relate these to the insulation structures for which the Weibull parameters have been experimentally determined. According to the transformer construction techniques, winding-to-ground stress applies to oil gaps and oil duct between barriers; intra-winding stress applies to turn-to-turn and coil-to-coil; inter-winding stress applies to oil gaps, oil duct between barriers, and coil-to-coil. For each set of structures considered for each stress, we select the worst values among all possible.
Remark: The values of the Weibull distribution provided by the literature, those in Tableau 1, are obtained with small test models that represent a piece of insulation of the whole system (the whole windings or the space between windings and tank/core); applying the experimental results obtained for pieces to the whole system is a question known as the “size effect” or the “enlargement law”. In most cases the problem comes down to the multiplication of the probabilities of failure of a series of N similar pieces of insulation, and in this case it can be shown that the Weibull distribution of the whole system has the same shape parameter as the pieces, only the scale parameter changes with N [35]. Yet the scale parameter, B in our expression (12), does not appear in our formulas of OV_capability_usage_ratio.
| Isolating structure type | Transformer type | n | k | m=n*k |
|---|---|---|---|---|
| Turn-to-turn | Core and shell | 44.9 47.1 | 0.42 0.43 | 18.9 20 |
| Coil-to-coil | Core | 39.9 43.2 | 0.40 0.43 | 16.0 18 |
| Shell | 32.6 - | 0.41 - | 13.4 - | |
| Oil duct between barriers | Core | 44.2 27.5 | 0.39 0.43 | 17.2 12 |
| Shell | 32.6 - | 0.41 - | 13.4 - |
3. Note on transformer overexcitation and surge arresters TOV withstand
As already mentioned, TOV may also generate thermal stresses which could lead to insulation damaging. Indeed, a power-frequency overvoltage generates an increase of the magnetic flux beyond the rated value, i. e. an overfluxing (or overexcitation), which in turn increases the eddy-current losses and may locally increase the temperature to a level that may damage the insulation. Yet this is less of a problem because transformer manufacturers are usually able to provide overfluxing capability curves. Some typical curves can also be in the literature [14][15][16][4][17].
These curves are in the form of voltage-time curves that provide the maximum voltage duration for a given voltage amplitude. Given that overfluxing is a thermal problem, these curves can be easily applied to time-varying amplitudes with the same “cumulative” procedure used for surge arresters [3]:
(23)
where dj and Vj have already been defined and D(Vj) is the duration given by the corresponding voltage-time curve for the voltage Vj. (Remember that this expression cannot be used for dielectric stress).
Note that voltage harmonics should be of little effect on the overexcitation phenomenon, the magnetic flux being inversely proportional to the voltage frequency (although a contribution is somewhat accounted for in the fact that Vj are peak values).
In addition to the transformers, it is important to consider the surge arresters nearby. Indeed, surge arresters are designed to limit lightning and switching overvoltages, not TOV; as a consequence, quite often their TOV withstand is lower than the phase-to-ground withstand of the transformer. There exist abundant literature about the surge arresters TOV withstand capability and how to evaluate the stress for a given overvoltage waveshape [18][19][20][3]. The TOV withstand voltage-time curve of a given surge arrester are standard data provided by the manufacturer.
These are the procedures used in the application example in §5 to compute the transformer overexcitation and surge arresters OV capability usage ratio.
4. Summary: Overall approach
The method we propose involves two steps. First, for the transformer at stake, we need to determine the withstand characteristics (curves/surfaces) associated to the dielectric tests, for each winding and for each pair of windings (e.g., for a single-phase transformer: HV, LV, HV/LV):
- Compute the Vwithstand duration D curves/surfaces, from the dielectric test levels and their duration D [LTAC, AV, IVW and IVPD tests] → expressions (7)(8)(9)
- Compute the Vwithstand,∞ curves/surfaces, from the highest voltage for the equipment, Um, associated to an infinite allowable duration → expressions (7)(8)(9)
Then we can compute the stress generated by the terminal overvoltages that were simulated or measured:
- Compute the dielectric stress as a function of time in each point of each winding and between each pair of points of each pair of windings, from the terminal voltages as a function of time → expressions (1)(2)(3) [x-position coordinates can be discretized into 100 points]
- Compute the envelopes of these stresses, {tj, Vj} (envelopes at power frequency, i. e. 50/60 Hz)
- Divide the curves {tj, Vj} into N segments {dj, Vj}, dk= tj- tj-1, j=1..N
- Compute the dielectric OV_capability_usage_ratio for each point of each winding and for each pair of points of each pair of windings → expression (22) [or (15) if using methods 1 or 2]
- The Weibull parameter values are provided in §2.6
- V0 is equal to Vwithstand,∞, determined from Um
[In some cases, for example with wye windings with the neutral solidly grounded, or when the withstand curves are not concave, considering only the voltages at the terminals may be enough and there is no need to consider all the points along the windings.]
- Compute the overexcitation and surge arresters OV_capability_usage_ratio → formula (23)
Result: the transformer withstand capability is not exceeded by the overvoltage only if OV_capability_usage_ratio≤1 for each point of each winding and for each pair of points of each pair of windings.

5. Application example and method comparison
The presented methods have been implemented in a computer program whose inputs are the transformer's dielectric test voltages and durations, its highest voltage for the equipment, Um, and the (simulated or measured) terminal overvoltages as a function of time. As an illustration, the figures below show the results obtained for an overvoltage generated when energizing a three-phase shell-type 100 MVA 400/8 kV YNd11 transformer. The Figure 5 left shows the phase-to-ground voltages at the transformer HV terminals.
Figure 5 right shows the OV_capability_usage_ratio in each part of the transformer at the end of the transient. For the dielectric stress, the method 3, contributions dependent on the memory effect, has been used here. The dielectric withstand capability of the transformer is exceeded for the insulation between the HV wye windings, where the usage ratio reaches 3.55 pu, i. e. 3.55 times the maximum allowed; and for the insulation between the LV delta windings, where the usage ratio reaches 1.12 pu. (The figure shows that the overvoltage withstand capability of the surge arresters is exceeded as well).
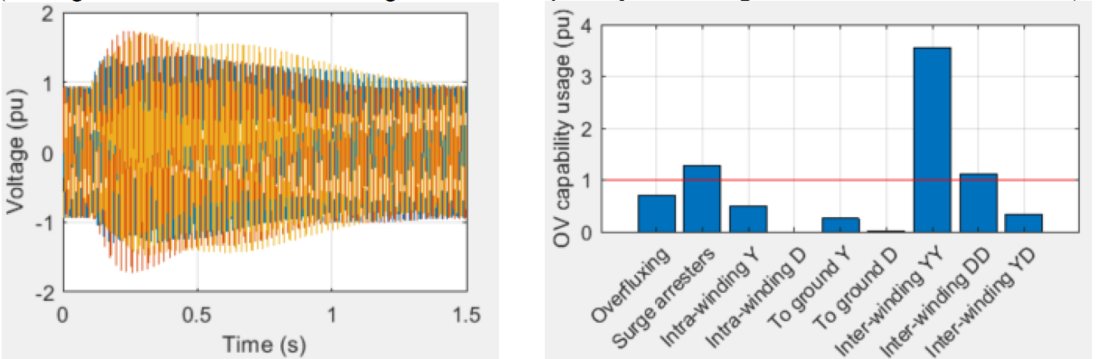
Figure 5 - Voltages at the transformer HV terminals (left); OV_capability_usage_ratio in each part of the transformer at the end of the transient (right)
Figure 6 provides complementary results on the dielectric stress between the HV windings. On the left, the spatial distribution of the dielectric usage ratio (at the end of the transient) between windings of phases B and C, which is maximum (3.55 pu) at xB=xC=1, i. e. between the winding terminals. On the right, the usage ratio between these two points (terminals B and C of the HV winding) against time, where we can see how the overvoltage increasingly consumes the dielectric withstand capability of the transformer insulation, the usage ratio reaching 3.55 pu at the end of the transient.
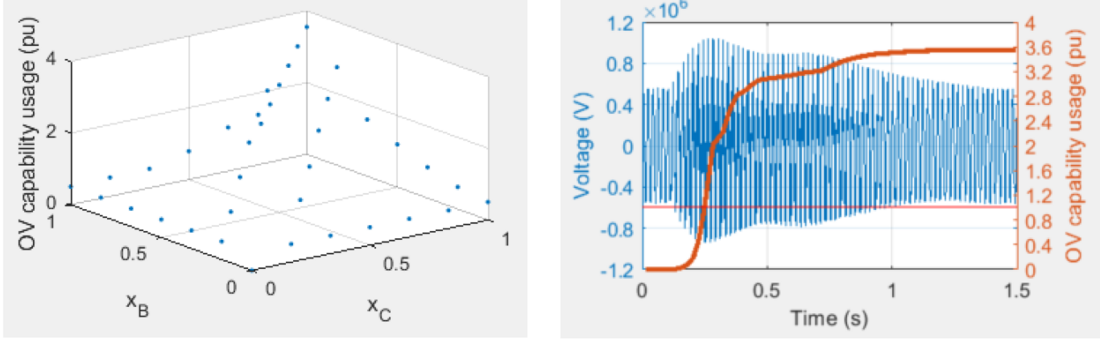
Figure 6 - OV_capability_usage_ratio between HV windings of phases B and C: spatial distribution at the end of the transient (left); value against time between points xB=xC=1, i. e. between terminals (right)
The table below shows the results with the other two methods, for three of the dielectric stresses. As expected, the method 1 leads to the highest values. The method 2 (with a wise choice of the similarity criterium value) and the method 3 lead to similar values, less overestimated than with method 1.
| Method 1 (independant segments) | Method 2 (independant groups of segments) | Method 3 (1%) (memory effect) | ||||
| 1% | 5% | 10% | 15% | |||
| Intra-winding Y | 88% | 70% | 55% | 50% | 40% | 50% |
| Intra-winding DD | 150% | 125% | 155% | 180% | 280% | 112% |
| Intra-winding YY | 480% | 440% | 330% | 260% | 310% | 355% |
6. Conclusion
The method we have presented in this paper allows to determine the TOV dielectric withstand capability for any transformer, provided its standard dielectric test levels are known. Our method accounts for the key factors we had identified: the interdependence between the withstand amplitude and duration, the time-varying amplitude of the overvoltages, the presence of harmonics and the insulation ageing. Of course, the “real” transformer TOV capability is probably higher than that associated to the dielectric test levels, but this cannot be determined without (very detailed) internal design data, which is almost never available.
The main theoretical principles of our method are the following: with TOV, the spatial voltage distributions inside the transformer are linear; the dielectric test voltages can be scaled to other amplitudes and durations with the V-t inverse power law; the withstand capability limit can be thought of as the probability of failure associated to the dielectric tests, which can be modelled by the Weibull law; the parameters of the V-t inverse power law and the Weibull failure probability laws are dimensionless and their values are found in the literature about the typical transformer insulating structures; the global effect of several voltage amplitudes can be computed by computing the failure probability associated to each constant-amplitude segment, taking into account the “memory effect” of the dielectrical withstand.
As a final remark, note that a similar procedure could be applied to determine the overvoltage withstand capability of other electrical machines such as generators and motors.
References
- IEC 60071-1:2006, Insulation co-ordination – Part 1: Definitions, principles, and rules.
- IEC TR 60071-4:2004, Insulation co-ordination – Part 4: Computational guide to insulation co-ordination and modelling of electrical networks.
- CIGRE WG 33.10, “Temporary Overvoltages: Causes, Effects and Evaluation”, Proceedings of the CIGRE 33rd Session, Paper 33-210, Paris, 1990.
- Adibi, M.M., R.W.Alexander and B.Avramovic, Power System Restoration Working Group, “Overvoltage Control During Restoration”, IEEE Transactions on Power Systems, Vol. 7, No. 4, pp. 1464-1470, Nov 1992.
- IEC 60076-3:2013 Power transformers – 3: Insulation levels, dielectric tests and external clearances in air.
- IEC 60071-2:2018 Insulation co-ordination - Part 2: Application guidelines.
- Balma P. M., R. C. Degeneff, H. R. Moore, L. B. Wagenaar, “The Effects of Long Term Operation and System Conditions on the Dielectric Capability and Insulation Coordination of Large Power Transformers”, IEEE Transactions on Power Delivery, Vol. 14, No. 3, July 1999.
- CIGRE WG 33.03, "Stresses in Metal Oxide Arresters Due to Temporary harmonic Overvoltages", Electra, pp. 79- 115, May 1990.
- Sybille, G.; Gavrilovic, M.M.; Belanger, J.; Do, V.Q., "Transformer Saturation Effects on EHV System Overvoltages", IEEE Trans. Power Apparatus and Systems, vol.PAS-104, no.3, pp.671-680, March 1985.
- CIGRE WG 33.06, "Metal oxide surge arresters in AC systems. Part 3: Temporary overvoltages and their stresses on metal oxide surge arresters", Electra 128, January 1990.
- Feltes, J. W., C. Grande-Moran, "Black Start Studies for System Restoration", Power System Dynamic Performance Committee, 2008 PES General Meeting July 20-24, 2008.
- Martínez Duró M., A. Tanguy, “Lack of Information about Transformer Dielectric Withstand to Harmonic Temporary Overvoltages”, Proceedings of the CIGRE Session, contribution to GDM, Paris, 2010.
- CIGRE WG C4.46, Evaluation of Temporary Overvoltages in Power Systems due to Low Order Harmonic Resonances, CIGRE TB 913, 2023.
- Alexander, G.W.; Corbin, S.L.; Mcnutt, W.J., "Influence of Design and Operating Practices on Excitation of Generator Step-Up Transformers," IEEE Trans. Power Apparatus and Systems, vol. 85, no.8, Aug. 1966.
- Gantner, J., F. H. Birch (WG 34-01), “Transformer overfluxing protection”, Electra 31, 1973.
- CIGRE WG 12-06, “Excitation of transformers”, Chapter 3 of Final Report, Electra 82, 1982.
- IEEE C37.91-2000, IEEE Guide for Protective Relay Applications to Power Transformers.
- IEC 60099-4:2009, Surge arresters – Part 4: Metal-oxide surge arresters without gaps for a.c. systems.
- IEC 60099-5:2000, Surge arresters – Part 5: Selection and application recommendations.
- IEEE C62.22-2009, IEEE Guide for the Application of Metal-Oxide Surge Arresters for AC Systems.
- CIGRE WG 33.10, “Temporary overvoltage withstand characteristics of extra high voltage equipment”, Electra 179, 1998, p. 38-49.
- Antonova, N.P, et al., “Temporary overvoltages and their influence upon the insulation level of the equipment”, CIGRE Session proceedings, v. 33, n. 209, p. 1-5, Paris, 1990.
- Langlois-Berthelot, R., Transformers and Generators for Power Systems. Their Behaviour, Capabilities and Rating, London, Macdonald, 1960.
- Blume, L. F., A. Boyajian; G. Camilli; T. C. Lennox; S. Minneci; V. M. Montsinger, Transformer Engineering, 2nd edition, John Wiley & Sons, Inc., New York, 1951.
- Yacov, S. et al., “Volt-time relationships for PDI in oil paper insulation", Electra 67, 1979.
- Ikeda M., S. Menju, "Breakdown Probability Distribution and Equi-probabilistic V-t Characteristics of Transformer Oil", IEEE Trans. Power Apparatus and Systems, PAS-98, No.4 July/Aug 1979.
- Harada, T.; Aihara, Y.; Kawamura, T.; Murano, M.; Ikeda, M.; Kumagai, S.; Inoue, Y.; Kamata, Y.; Matsuura, K.; Watanabe, T.; Sugimoto, T., "Short Time Ac V-t Characteristics of Oil Gaps," IEEE Trans. Dielectr. Electr. Insul., vol.EI-16, no.5, pp.423,430, Oct. 1981.
- Tsuboi, T.; Takami, J.; Okabe, S.; Inami, K.; Aono, K., "Transformer insulation reliability for moving oil with Weibull analysis," Dielectrics and Electrical Insulation, IEEE Trans., vol.17, no.3, pp.978,983, June 2010.
- Ikeda M., T. Yanari, and H. Okubo, “PD and BD Probability Distribution and Equi-Probabilistic V-t Characteristics of Oil-filled Transformer Insulation”, IEEE Trans. Power App. Syst., Vol. 101, pp. 2728-2735, 1982.
- Okabe, S., T. Ohno and E. Zaima: “V-t and V-N Characteristics of Insulation Elements with Large Scale Oil-Immersed Transformers”, 14th International Symposium on High Voltage Engineering, Paper I-13, 2005.
- Okabe S., “Voltage-time and Voltage-Number Characteristics of Insulation Elements with Oil-Filled Transformers in EHV and UHV Classes”, IEEE Trans. Dielectr. Electr. Insul. Vol. 13, pp. 436-444, 2006.
- Okabe, S.; Tsuboi, T.; Takami, J., "Reliability evaluation with Weibull distribution on AC withstand voltage test of substation equipment," IEEE Trans. Dielectr. Electr. Insul. vol.15, no.5, pp.1242,1251, October 2008.
- Hirose, H., “A Method to Estimate the Lifetime of Solid Electrical Insulation”, IEEE Trans. Electr. Insul, Vol. 22, pp. 745-753, 1987.
- Brown, G. W., "The Weibull distribution: Some Dangers with its Use in Insulation Studies," IEEE Trans. Power Apparatus and Systems, vol.PAS-101, no.9, pp.3513,3522, Sept. 1982.
- Hauschild, W., & Mosch, W., Statistical Techniques for High-Voltage Engineering, IET, 2007.
- Montanari, G.C., "Electrical life threshold models for solid insulating materials subjected to electrical and multiple stresses. I. Investigation and comparison of life models," IEEE Trans. Electrical Insulation, vol.27, no.5, pp. 974-986, Oct. 1992.
- Montsinger, V.M, “Effects of time and frequency on insulation test of transformers”, AIEE Transactions, Vol. 43, February 1924, pp. 337–347.
- Vogel, F.J, “Insulation tests of transformers as influenced by time and frequency”, AIEE Transactions, Vol. 43, February 1924, pp. 348–355.

- [1] It should be noticed that the voltages at the terminals of the windings are: for terminals connected to an external network (a power source; earth), the voltage of this network at the point of connection; for the terminals not connected to an external network, the induced voltages, which depend on the type of core (single-phase or three-phase, zero sequence flux return leg or not), the coupling of the windings, and the vector index of the transformer.
